Dane:
d = 1 m
f1 = 1,5 Hz
f2 = 5 Hz
∆t = 4 s
niech ![]()
wiemy, że:
![]()
![]()
![]()
Pień staczając się, wykonuje ruch postępowy oraz ruch obrotowy
Na pień działa siła ciężkości, siła tarcia i siła reakcji podłoża.
Rozpisując siłę ciężkości na składowe:
![]()
![]()
![]()
![]()
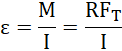
Moment bezwładności walca: ![]()
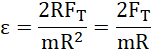
co daje:
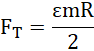
wstawiając do pierwszej równości:
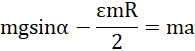
po przekształceniach:
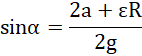
wiedząc, że ![]()
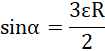
a ponieważ ![]()
![]()
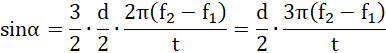
![]()
![]()
Odpowiedź: Kąt nachylenia zbocza to około 25 stopni.

Przypomnij sobie wzór na prędkość kątową z wykorzystaniem częstotliwości. Następnie zastanów się, jakie siły działają na pień – są to siła ciężkości, siła reakcji podłoża oraz siła tarcia. Rozpisując siłę ciężkości na składowe, zauważ, że jedna z nich równoważy się z siłą reakcji podłoża. Wypadkowa pozostałych sił to z drugiej zasady dynamiki dla ruchu postępowego, iloczyn masy i przyspieszenia. Pień obraca się, więc z drugiej zasady dynamiki dla ruchu obrotowego, przyspieszenie kątowe jest równe ilorazowi wypadkowej momentu sił (tutaj jest to moment siły tarcia) i momentu bezwładności walca (odczytaj z tabeli na końcu zbioru zadań). Z drugiej równości wyznacz siłę tarcia i wstaw ją do pierwszego wyrażenia. Wyznacz z niego sinus kąta alfa i zastanów się, jakie wartości są wciąż nieznane – przyspieszanie kątowe to iloraz prędkości kątowej i czasu – z danych częstotliwości poznasz prędkość, a więc i przyspieszenie, przyspieszenie liniowe to z kolei iloczyn przyspieszenia kątowego i promienia pnia. Wylicz przybliżoną wartość sinusa i odszukaj wartość kąta w tablicach trygonometrycznych.