Dane:
α = 30°
M = 200 kg
t = 2 s
μ = 0,4
m = 5 kg
Aby poznać długość równi, potrzebujemy obliczyć wartość przyspieszenia liniowego, wtedy ![]()
Na skrzynię działa siła grawitacji, siła tarcia, siła naciągu liny oraz siła reakcji podłoża.
Rozłóżmy siłę grawitacji na składowe:
![]()
![]()
![]()
![]()
co daje:
![]()
na bęben działa siła naciągu liny, z 2 zasady dynamiki w ruchu obrotowym dla bryły sztywnej:
![]()
moment bezwładności walca: ![]()
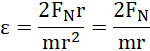
ponadto:
![]()
więc:
![]()
po przyrównaniu do siebie:
![]()

a więc:
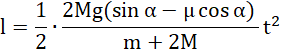
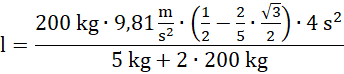
![]()
Odpowiedź: Równia ma 3 metry długości.

Wiesz, że skrzynia porusza się ruchem jednostajnie przyspieszonym, więc długość równi możesz wyliczyć ze wzoru na drogę w ruchu liniowym jednostajnie zmiennym – znasz czas ruchu, pozostaje wyliczyć przyspieszenie liniowe skrzyni. Na początek zastanów się jakie siły działają na skrzynię, a jakie – na bęben wciągarki. Na skrzynie oczywiście działa siła grawitacji działająca pionowo w dół (musisz rozpisać ją na składowe – siłę o kierunku wzdłuż równi oraz siłę do niej prostopadłą), siła tarcia siła i siła naciągu liny – obie działające wzdłuż równi o zwrocie przeciwnym do ruchu skrzyni, oraz siła reakcji podłoża o kierunku prostopadłym do równi zwrócona w górę. Zapisz wypadkową tych sił – z 2. zasady dynamiki dla ruchu prostoliniowego jest to iloczyn masy i przyspieszenia liniowego (zwróć uwagę, siła reakcji podłoża redukuje się z jedną ze składowych siły ciężkości – nie musisz uwzględniać ich przy składaniu sił). Teraz skup się na sile naciągu liny działającej na bęben – wprawia ona go w ruch obrotowy, więc z 2 zasady dynamiki dla ruchu obrotowego możesz zapisać, że iloraz momentu siły i momentu bezwładności to przyspieszenie kątowe walca. Następnie skorzystaj z zależności między prędkością kątową i liniową i z zebranych równości wyznacz siłę naciągu liny. Po przyrównaniu do siebie wyrażeń możesz wyliczyć przyspieszenie liniowe.