Dane:
R
m1
m2
I
Niech zwrot osi układu współrzędnych będzie zwrócony w dół.
Dla ciężarka po lewej stronie:
![]()
Dla ciężarka po prawej stronie:
![]()
Dla bloku:
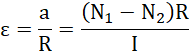
Wyliczmy przyspieszenie a:
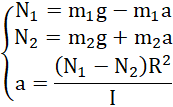
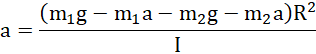
Po przeniesieniu na jedną stronę niewiadomej a, wyłączeniu jej przed nawias i wykonaniu dzielenia:
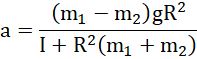
Wyliczmy siły naciągu nitki:
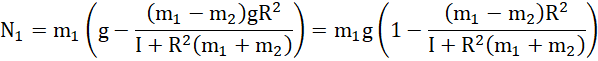
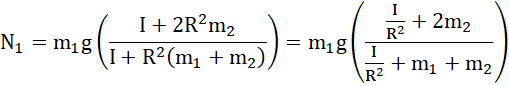
W analogiczny sposób:
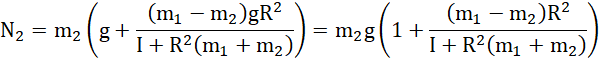
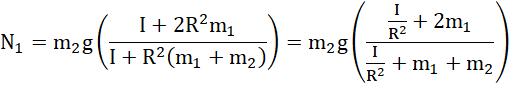

Na początek ustal zwrot osi układu współrzędnych. Następnie, wykorzystując drugą zasadę dynamiki dla ruchu postępowego, zapisz równania sił dla każdego ciężarka (zwróć uwagę na znaki przy siłach, zależą one od ustalonego zwrotu układu współrzędnych oraz od tego, jak będzie poruszać się ciężarek – cięższy opadnie w dół, a lżejszy poruszy się do góry). Korzystając z drugiej zasady dynamiki dla ruchu obrotowego, zapisz równość pomiędzy przyspieszeniem kątowym (te z kolei zamień na iloraz przyspieszenia liniowego i promienia) a wypadkowym momentem sił naciągu (jest to różnica tych sił) i momentem bezwładności. Z zebranych równości wyznacz najpierw przyspieszenie liniowe – wyznacz siły naciągu z dwóch pierwszych równości, wstaw je do trzeciego równania i wykonaj konieczne przekształcenia. Otrzymane przyspieszenie wstaw do pierwszych równań.