Dane:
L = 70 cm = 0,7 m
f = 10 Hz
![]()
![]()
![]()
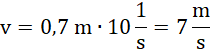
Odpowiedź: Prędkość liniowa punktu położonego najdalej od osi obrotu piłki wynosi 7![]()
Wykres zależności prędkości liniowej od odległości od osi obrotu:
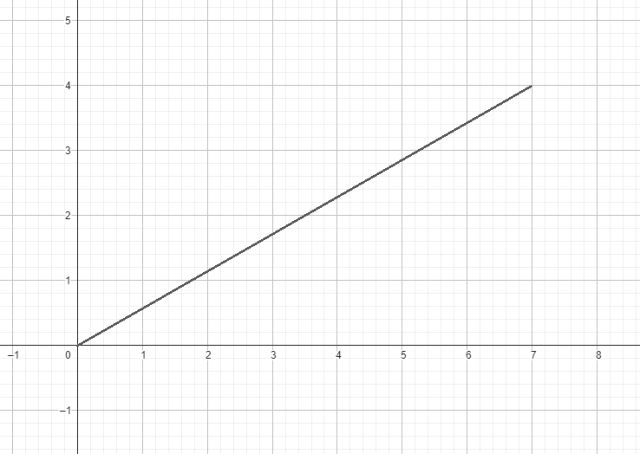
wykres zależności prędkości kątowej od odległości od osi obrotu:
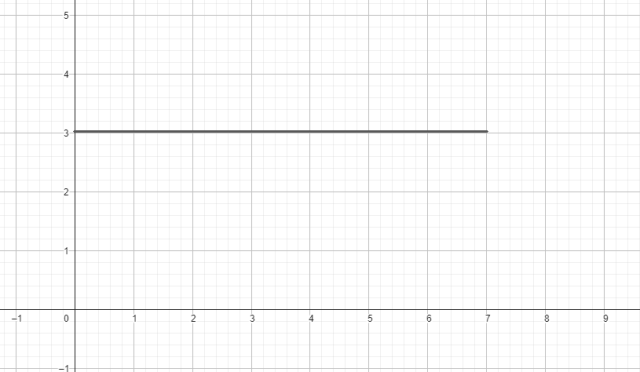

Pamiętaj, prędkość liniową otrzymasz, mnożąc odległość od osi obrotu przez prędkość kątową. Wartość ta nie jest jednak podana w zadaniu – wyliczysz ją, mnożąc 2π przez częstotliwość ruchu. Następnie zauważ, 2πr, które pojawiło się w trakcie obliczeń to właśnie obwód okręgu – zastąp ten czynnik przez L. Zastanów się jak na zmianę wyniku wpłynęłaby zmiana promienia r – czynnik ten występuje w pierwszej potędze, więc jest on liniowy – zmniejszenie/zwiększenie go x razy spowoduje zwiększenie/zmniejszenie wyniku x razy – oznacza to, że wykres będzie funkcją liniową o początku w punkcie (0,0). Odległość od środka piłki nie wpływa za to na prędkość kątową – we wzorze nie występuje bowiem promień – wykres będzie funkcją stałą.