W tym zadaniu musisz obliczyć kąt BAC w trójkącie równoramiennym ABC, korzystając z twierdzenia cosinusów.
|AB| = |AC| = √3 cm, |BC| = 3 cm
|AB| = b, |AC| = c, |BC| = a
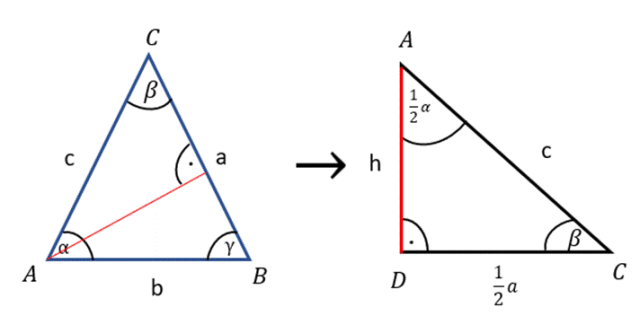
Rysunek poglądowy:
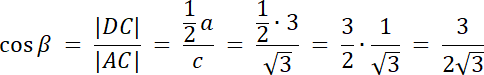
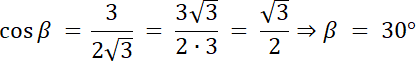
Suma kątów w trójkącie = 180°, więc
![]() α + 90° + 30° = 180°
α + 90° + 30° = 180°
![]() α + 120° = 180° |–120°
α + 120° = 180° |–120°
![]() α = 60° |∙2
α = 60° |∙2
α = 120°

W pierwszym kroku poprowadź wysokość z wierzchołka A. Zauważ, że skoro trójkąt jest równoramienny to wysokość poprowadzona z wierzchołka, będącego naprzeciwko podstawy trójkąta, dzieli podstawę na dwa równe odcinki, oraz kąt BAC na dwie równe części. Na rysunku z prawej strony, widzimy powstały trójkąt prostokątny. Następnie z funkcji cosinus wyznacz kąt β i skorzystaj z własności na sumę kątów w trójkącie, by wyznaczyć wartość kąta α.

Ćwiczenie 1.
219Ćwiczenie 2.
221Zadanie 1.
222Zadanie 2.
222Zadanie 3.
222Ćwiczenie 1.
225Zadanie 1.
226Zadanie 2.
226Zadanie 3.
226Ćwiczenie 1.
228Zadanie 1.
232Zadanie 5.
232Zadanie 6.
232Zadanie 7.
232Zadanie 1.
236Zadanie 2.
236Ćwiczenie 6.
240Zadanie 1.
240Zadanie 3.
241Zadanie 4.
241Zadanie 5.
241Zadanie 6.
241Zadanie 10.
241Zadanie 11.
241Zadanie 12.
241Zadanie 13.
241Ćwiczenie 2.
243Zadanie 1.
245Zadanie 2.
246Zadanie 3.
246Zadanie 4.
246Zadanie 5.
246Zadanie 6.
246Zadanie 7.
246Zadanie 8.
246Zadanie 3.
249Zadanie 7.
249Ćwiczenie 2.
251Zadanie 5.
253Zadanie 6.
253Zadanie 16.
254Zadanie 17.
254Zadanie 11.
260Zadanie 13.
260Zadanie 14.
260Zadanie 18.
260Zadanie 19.
260Zadanie 20.
260Zadanie 21.
260Zadanie 22.
261Zadanie 24.
261Zadanie 30.
261
