W tym zadaniu musisz wyznaczyć na dwa sposoby promie okręgu wpisanego w trójkąt ABC.
Rysunek poglądowy:
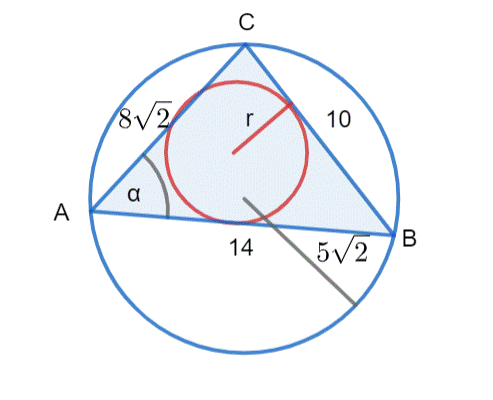
Przyjmij: r–promień okręgu wpisanego w trójkąt ABC, |∡BAC| = α
Z podpunktu 1, wiemy, że α = 45°.
Metoda nr 1:
P = r∙0,5obw, gdzie: P–pole, obw–obwód, r–promień okręgu wpisanego w trójkąt
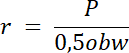
obw = |AB| + |BC| + |CA|
obw = 14 + 10 + 8√2
obw = 8(3 + √2) /2
0,5obw = 4(3 + √2)
PABC = 56
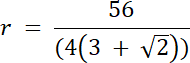
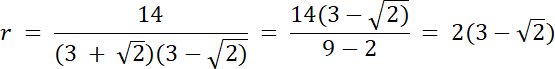
Metoda nr 2:
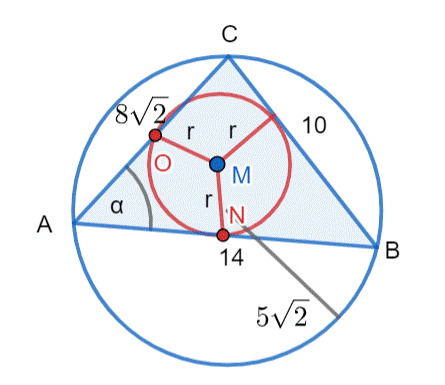
PABC = PABM + PBCM + PACM
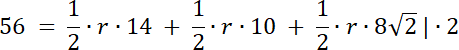
112 = 14r + 10r + 8√2r
112 = 24r + 8√2r
112 = 8r(3 + √2) | /8(3 + √2)
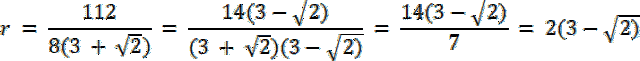

W tym zadaniu skorzystaj z twierdzenia na promień okręgu wpisanego w trójkąt, który wykorzystuje pole i obwód tego trójkąta. Z kolei, w drugiej metodzie wykorzystaj własność okręgu wpisanego w trójkąt–promień okręgu, jest wysokością trzech trójkątów, które postały po wyprowadzeniu promieni ze środka okręgu.

Ćwiczenie 1.
219Ćwiczenie 2.
221Zadanie 1.
222Zadanie 2.
222Zadanie 3.
222Ćwiczenie 1.
225Zadanie 1.
226Zadanie 2.
226Zadanie 3.
226Ćwiczenie 1.
228Zadanie 1.
232Zadanie 5.
232Zadanie 6.
232Zadanie 7.
232Zadanie 1.
236Zadanie 2.
236Ćwiczenie 6.
240Zadanie 1.
240Zadanie 3.
241Zadanie 4.
241Zadanie 5.
241Zadanie 6.
241Zadanie 10.
241Zadanie 11.
241Zadanie 12.
241Zadanie 13.
241Ćwiczenie 2.
243Zadanie 1.
245Zadanie 2.
246Zadanie 3.
246Zadanie 4.
246Zadanie 5.
246Zadanie 6.
246Zadanie 7.
246Zadanie 8.
246Zadanie 3.
249Zadanie 7.
249Ćwiczenie 2.
251Zadanie 5.
253Zadanie 6.
253Zadanie 16.
254Zadanie 17.
254Zadanie 11.
260Zadanie 13.
260Zadanie 14.
260Zadanie 18.
260Zadanie 19.
260Zadanie 20.
260Zadanie 21.
260Zadanie 22.
261Zadanie 24.
261Zadanie 30.
261
