W tym zadaniu musisz udowodnić, że środkowa trójkąta, dzieli trójkąt tak, że powstałe po podziale trójkąty mają równe pola.
Rysunek poglądowy:
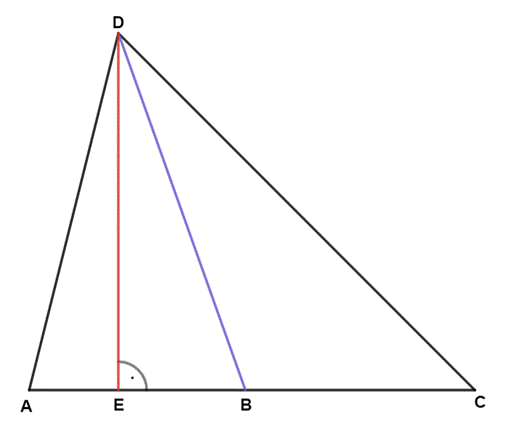
|BD|–środkowa trójkąta ACD, |DE|–wysokość trójkąta ACD, więc:
|AC| = |AB| + |BC| i |AB| = |BC|
Przyjmij: |AB| = a, |BC| = b⇒ a = b
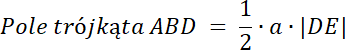
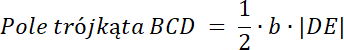
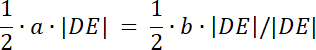
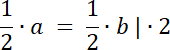
a = b, więc
PABD = PBCD

Narysuj trójkąt, wysokość oraz środkową w tym trójkącie i oznacz na nim wierzchołki. Następnie wyprowadź zależność na długość boku, który został podzielony po wyprowadzeniu do niego środowej BD. Policz pola nowo powstałych trójkątów–zauważ, że mają one wysokość o takiej samej długości i sprawdź słuszność dowodu.

Ćwiczenie 1.
219Ćwiczenie 2.
221Zadanie 1.
222Zadanie 2.
222Zadanie 3.
222Ćwiczenie 1.
225Zadanie 1.
226Zadanie 2.
226Zadanie 3.
226Ćwiczenie 1.
228Zadanie 1.
232Zadanie 5.
232Zadanie 6.
232Zadanie 7.
232Zadanie 1.
236Zadanie 2.
236Ćwiczenie 6.
240Zadanie 1.
240Zadanie 3.
241Zadanie 4.
241Zadanie 5.
241Zadanie 6.
241Zadanie 10.
241Zadanie 11.
241Zadanie 12.
241Zadanie 13.
241Ćwiczenie 2.
243Zadanie 1.
245Zadanie 2.
246Zadanie 3.
246Zadanie 4.
246Zadanie 5.
246Zadanie 6.
246Zadanie 7.
246Zadanie 8.
246Zadanie 3.
249Zadanie 7.
249Ćwiczenie 2.
251Zadanie 5.
253Zadanie 6.
253Zadanie 16.
254Zadanie 17.
254Zadanie 11.
260Zadanie 13.
260Zadanie 14.
260Zadanie 18.
260Zadanie 19.
260Zadanie 20.
260Zadanie 21.
260Zadanie 22.
261Zadanie 24.
261Zadanie 30.
261
