W tym zadaniu musisz obliczyć pole, czwartego trójkąta, który powstał po podziale czworokąta na cztery części.
Rysunek pomocniczy:
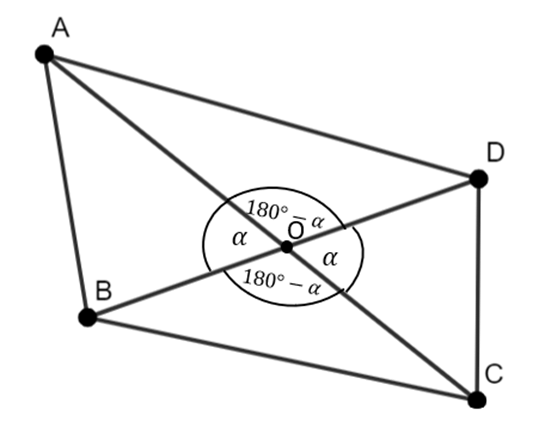
Rozwiązanie nr 1:
PABO = 20
PBCO = 30
PCDO = 40
Przyjmij:
|AO| = a, |BO| = b, |OC| = c, |OD| = d,
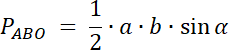
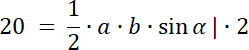
![]()
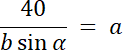
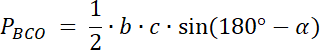
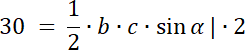
![]()
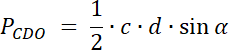
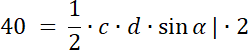
![]()
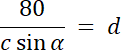
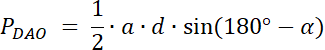
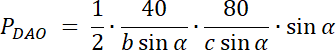
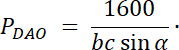
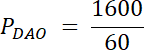
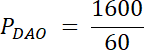
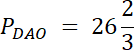
Rozwiązanie nr 2:
PABO = 40
PBCO = 20
PCDO = 30
Przyjmij:
|AO| = a, |BO| = b, |OC| = c, |OD| = d
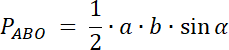
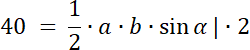
![]()
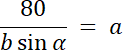
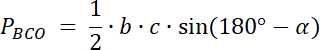
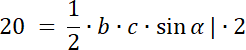
![]()
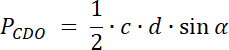
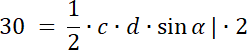
![]()
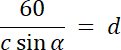
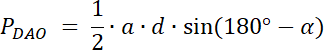
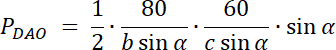
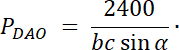
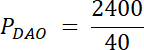
![]()
Rozwiązanie nr 3:
PABO = 30
PBCO = 40
PCDO = 20
Przyjmij:
|AO| = a, |BO| = b, |OC| = c, |OD| = d
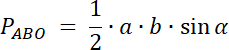
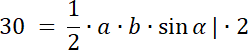
![]()
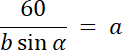
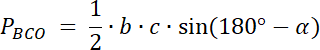
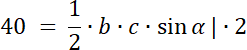
![]()
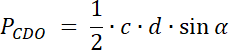
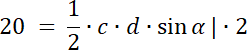
![]()
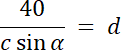
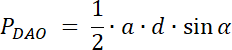
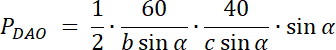
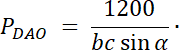
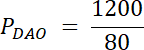
![]()

W pierwszym kroku narysuj ten czworokąt, zaznacz na nim powstałe trójkąty oraz wypisz ich kąty wierzchołkowe. Pole każdego z nich wyznacz ze wzoru na pole trójkąta, który wykorzystuje funkcję sinus. Kąty wierzchołkowe leżące naprzeciwko siebie mają taką samą miarę. Wyznacz wartości boków dla szukanego trójkąta i oblicz jego pole. Zadanie ma 3 rozwiązania–każdy z 3 wiadomych trójkątów ma pole 20 lub 30, lub 40–stwórz 3 kombinację.

Ćwiczenie 1.
219Ćwiczenie 2.
221Zadanie 1.
222Zadanie 2.
222Zadanie 3.
222Ćwiczenie 1.
225Zadanie 1.
226Zadanie 2.
226Zadanie 3.
226Ćwiczenie 1.
228Zadanie 1.
232Zadanie 5.
232Zadanie 6.
232Zadanie 7.
232Zadanie 1.
236Zadanie 2.
236Ćwiczenie 6.
240Zadanie 1.
240Zadanie 3.
241Zadanie 4.
241Zadanie 5.
241Zadanie 6.
241Zadanie 10.
241Zadanie 11.
241Zadanie 12.
241Zadanie 13.
241Ćwiczenie 2.
243Zadanie 1.
245Zadanie 2.
246Zadanie 3.
246Zadanie 4.
246Zadanie 5.
246Zadanie 6.
246Zadanie 7.
246Zadanie 8.
246Zadanie 3.
249Zadanie 7.
249Ćwiczenie 2.
251Zadanie 5.
253Zadanie 6.
253Zadanie 16.
254Zadanie 17.
254Zadanie 11.
260Zadanie 13.
260Zadanie 14.
260Zadanie 18.
260Zadanie 19.
260Zadanie 20.
260Zadanie 21.
260Zadanie 22.
261Zadanie 24.
261Zadanie 30.
261
