W tym zadaniu oblicz pole wycinka koła.
R–promień wycinka koła, r–promień okręgu wpisanego okręgu.
Rysunek pomocniczy:
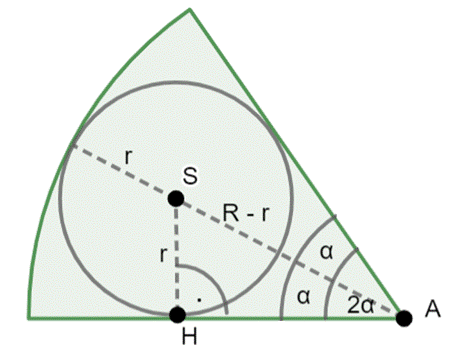
Trójkąt HAS:
|SH| = r = 3 cm
|AS| = R–r = 9–3 = 6 cm
PHAS = 0,5∙|AH|∙r
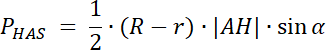
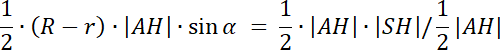
6∙sin α = 3 /6
sin α = 0,5
α = 30°, bo trójkąt HAS jest prostokątny
2α = 2∙30° = 60°
![]()
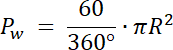
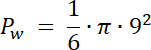
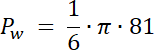
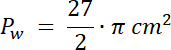
Pw = 13,5 cm2

Narysuj wycinek koła, zaznacz na rysunku promień okręgu wpisanego i wyprowadź promień wycinka koła z punktu A. Zauważ, że promień R i r przecinają się w punkcie S, tworząc trójkąt HAS. Wyznacz pole tego trójkąta–i na jego podstawie określ kąt leżący naprzeciwko boku |HS|, czyli promienia okręgu wpisanego. Kąt |∡A| = 2α, a na podstawie tego wyrażenia, wyznacz pole wycinka koła.

Ćwiczenie 1.
219Ćwiczenie 2.
221Zadanie 1.
222Zadanie 2.
222Zadanie 3.
222Ćwiczenie 1.
225Zadanie 1.
226Zadanie 2.
226Zadanie 3.
226Ćwiczenie 1.
228Zadanie 1.
232Zadanie 5.
232Zadanie 6.
232Zadanie 7.
232Zadanie 1.
236Zadanie 2.
236Ćwiczenie 6.
240Zadanie 1.
240Zadanie 3.
241Zadanie 4.
241Zadanie 5.
241Zadanie 6.
241Zadanie 10.
241Zadanie 11.
241Zadanie 12.
241Zadanie 13.
241Ćwiczenie 2.
243Zadanie 1.
245Zadanie 2.
246Zadanie 3.
246Zadanie 4.
246Zadanie 5.
246Zadanie 6.
246Zadanie 7.
246Zadanie 8.
246Zadanie 3.
249Zadanie 7.
249Ćwiczenie 2.
251Zadanie 5.
253Zadanie 6.
253Zadanie 16.
254Zadanie 17.
254Zadanie 11.
260Zadanie 13.
260Zadanie 14.
260Zadanie 18.
260Zadanie 19.
260Zadanie 20.
260Zadanie 21.
260Zadanie 22.
261Zadanie 24.
261Zadanie 30.
261
