W tym zadaniu wyznacz długość boku c oraz kąty β, γ.
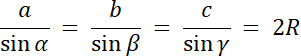
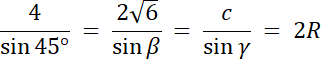
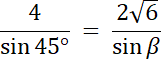
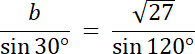
![]()
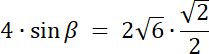
![]()
![]()
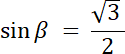
β = 60° v β = 120°
Przypadek nr 1: β = 60°
α + β + γ = 180°
45° + 60° + γ = 180°
105° + γ = 180° |–105°
γ = 75°
![]()
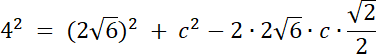
![]()
![]()
![]()
![]()
![]()
![]()
![]()
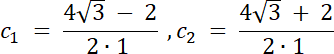
![]()
c2 < b–więc c2 sprzeczne, ponieważ c–najdłuższy bok trójkąta–leży naprzeciwko największego kąta
![]()
Przypadek nr 2: β = 120°
α + β + γ = 180°
45° + 120° + γ = 180°
165° + γ = 180° |–165°
γ = 15°
![]()
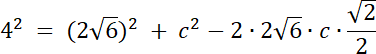
![]()
![]()
![]()
![]()
![]()
![]()
![]()
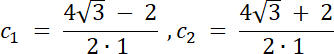
![]()
c2 > b–więc c1 sprzeczne, ponieważ c–najkrótszy bok trójkąta–leży naprzeciwko najmniejszego kąta
![]()
Rozwiązania:
β = 60°, γ = 75°, c = 2√3 + 1
β = 120°, γ = 15°, c = 2√3–1

Skorzystaj z sumy kątów w trójkącie, twierdzenia sinusów i twierdzenia cosinusów, aby wyznaczyć brakujące wartości liczbowe boku oraz kątów w trójkącie.

Ćwiczenie 1.
219Ćwiczenie 2.
221Zadanie 1.
222Zadanie 2.
222Zadanie 3.
222Ćwiczenie 1.
225Zadanie 1.
226Zadanie 2.
226Zadanie 3.
226Ćwiczenie 1.
228Zadanie 1.
232Zadanie 5.
232Zadanie 6.
232Zadanie 7.
232Zadanie 1.
236Zadanie 2.
236Ćwiczenie 6.
240Zadanie 1.
240Zadanie 3.
241Zadanie 4.
241Zadanie 5.
241Zadanie 6.
241Zadanie 10.
241Zadanie 11.
241Zadanie 12.
241Zadanie 13.
241Ćwiczenie 2.
243Zadanie 1.
245Zadanie 2.
246Zadanie 3.
246Zadanie 4.
246Zadanie 5.
246Zadanie 6.
246Zadanie 7.
246Zadanie 8.
246Zadanie 3.
249Zadanie 7.
249Ćwiczenie 2.
251Zadanie 5.
253Zadanie 6.
253Zadanie 16.
254Zadanie 17.
254Zadanie 11.
260Zadanie 13.
260Zadanie 14.
260Zadanie 18.
260Zadanie 19.
260Zadanie 20.
260Zadanie 21.
260Zadanie 22.
261Zadanie 24.
261Zadanie 30.
261
