W tym zadaniu, należy wyznaczyć stosunek pola trójkąta odciętego przez prostą do pola trójkąta ABC
Rysunek pomocniczy:
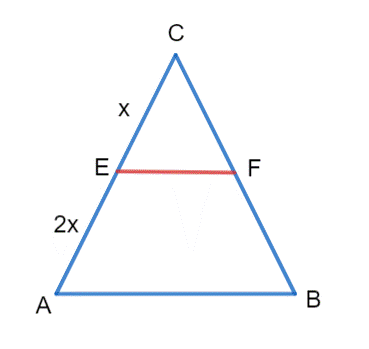
x–długość odcinka |CE|
2x–długość odcinka |AE|
k–skala podobieństwa
Z podobieństwa trójkątów ABC i CEF, otrzymasz:
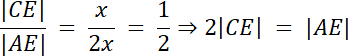
|AB| = |AE| + |CE|
|AB| = 2x + x⇒ |AB| = 3x
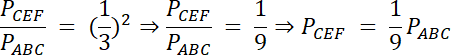

W tym zadaniu, najpierw wyznacz stosunek odcinka |CE| do |AE|, a następnie z twierdzenia o stosunku pól figur podobnych, wyznacz jaką cześć trójkąta ABC, stanowi trójkąt powstały po przeprowadzeniu równoległej przez trójkąt ABC.

Ćwiczenie 1.
219Ćwiczenie 2.
221Zadanie 1.
222Zadanie 2.
222Zadanie 3.
222Ćwiczenie 1.
225Zadanie 1.
226Zadanie 2.
226Zadanie 3.
226Ćwiczenie 1.
228Zadanie 1.
232Zadanie 5.
232Zadanie 6.
232Zadanie 7.
232Zadanie 1.
236Zadanie 2.
236Ćwiczenie 6.
240Zadanie 1.
240Zadanie 3.
241Zadanie 4.
241Zadanie 5.
241Zadanie 6.
241Zadanie 10.
241Zadanie 11.
241Zadanie 12.
241Zadanie 13.
241Ćwiczenie 2.
243Zadanie 1.
245Zadanie 2.
246Zadanie 3.
246Zadanie 4.
246Zadanie 5.
246Zadanie 6.
246Zadanie 7.
246Zadanie 8.
246Zadanie 3.
249Zadanie 7.
249Ćwiczenie 2.
251Zadanie 5.
253Zadanie 6.
253Zadanie 16.
254Zadanie 17.
254Zadanie 11.
260Zadanie 13.
260Zadanie 14.
260Zadanie 18.
260Zadanie 19.
260Zadanie 20.
260Zadanie 21.
260Zadanie 22.
261Zadanie 24.
261Zadanie 30.
261
