W tym zadaniu wyznacz wartość funkcji sinus, dla najmniejszego kąta, w tym trójkącie.
Rysunek poglądowy:
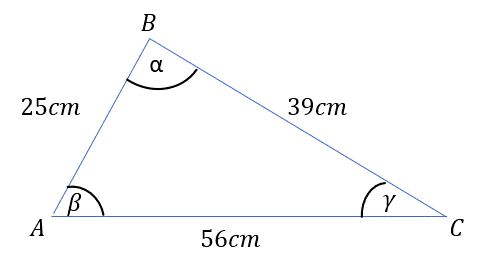
przyjmij:
|∡ABC| = α, |∡BAC| = β, |∡ACB| = γ,
Z podpunktu a:
P–pole trójkąta i P = 420 cm2
Z podpunktu b:
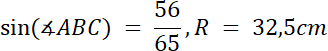
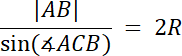
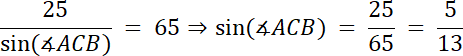
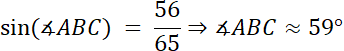
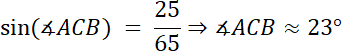
![]()
![]()
![]()
Najmniejszy kąt: |∡ACB| ≈ 23°
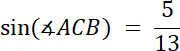

W tym zadaniu musisz najpierw obliczyć wartość kątów w trójkącie–na tej podstawie ustal, których z nich ma najmniejszą miarę, a następnie wyznacz funkcję sinus tego kąta–wykorzystaj do tego twierdzenie sinusów.

Ćwiczenie 1.
219Ćwiczenie 2.
221Zadanie 1.
222Zadanie 2.
222Zadanie 3.
222Ćwiczenie 1.
225Zadanie 1.
226Zadanie 2.
226Zadanie 3.
226Ćwiczenie 1.
228Zadanie 1.
232Zadanie 5.
232Zadanie 6.
232Zadanie 7.
232Zadanie 1.
236Zadanie 2.
236Ćwiczenie 6.
240Zadanie 1.
240Zadanie 3.
241Zadanie 4.
241Zadanie 5.
241Zadanie 6.
241Zadanie 10.
241Zadanie 11.
241Zadanie 12.
241Zadanie 13.
241Ćwiczenie 2.
243Zadanie 1.
245Zadanie 2.
246Zadanie 3.
246Zadanie 4.
246Zadanie 5.
246Zadanie 6.
246Zadanie 7.
246Zadanie 8.
246Zadanie 3.
249Zadanie 7.
249Ćwiczenie 2.
251Zadanie 5.
253Zadanie 6.
253Zadanie 16.
254Zadanie 17.
254Zadanie 11.
260Zadanie 13.
260Zadanie 14.
260Zadanie 18.
260Zadanie 19.
260Zadanie 20.
260Zadanie 21.
260Zadanie 22.
261Zadanie 24.
261Zadanie 30.
261
