W tym zadaniu musisz obliczyć pole figury, będące częścią wspólną pól okręgów o środach w punktach A i C.
Rysunek pomocniczy:
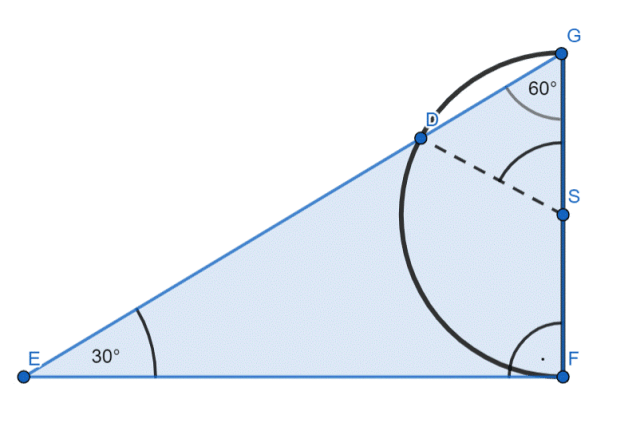
|GF| = 2, |SG| = 0,5|GF|, |∡E| = 30°, |∡G| = 60°
Pn–pole figury zamalowanej na niebiesko
Pw–pole wycinka kołowego S
Pw2–pole wycinka kołowego o środku SDG
Ptr–pole trójkąta równobocznego, o boku a
PEFG–połowa trójkąta równoramiennego o boku = a, gdzie a = 2∙2 = 4
|SG| = promień zakreślonego koła
|EF| = 2√3
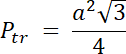
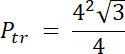
![]()
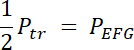
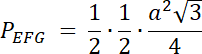
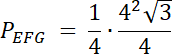
![]()
|∡S| = 60°, |SG| = | DS| = r; r = 0,5∙2, r = 1
|∡DSF| = 120°
Pole wycinka kołowego o środku S:
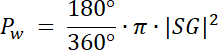
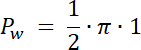
![]()
Pole wycinka kołowego SDG:
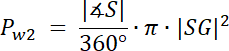
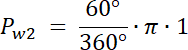
![]()
Trójkąt SGD:
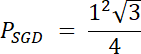
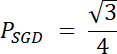
Pole figury DG:–PDG
PDG = Pw2–PSGD
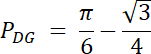
Pole niebieskiej figury EFD:
PEFD = PEFG–Pw–PDG
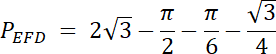
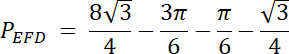
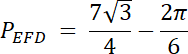
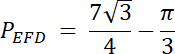
Długość łuku DF:
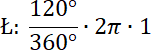
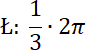
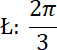
|ED| = |EG|–|DG|
|ED| = 4–1
|ED| = 3
Obwód figury niebieskiej figury EFD:
LEFD = |EF| + DF + |ED|
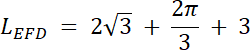

W pierwszym kroku opisz dobrze dane dla tej figury, zauważ również, z jakich figur geometrycznych się składa. W celu obliczenia pola figury zamalowanej na niebiesko zauważ, że trójkąt EFG to połowa trójkąta równobocznego, a pole figury DG powstaje po odjęciu od pola wycinka kołowego: SDG, trójkąta równobocznego SGD. Z kolei, aby obliczyć obwód, zauważ, że jest to: suma długości łuku FD i boki: |EF| + |ED|.

Ćwiczenie 1.
219Ćwiczenie 2.
221Zadanie 1.
222Zadanie 2.
222Zadanie 3.
222Ćwiczenie 1.
225Zadanie 1.
226Zadanie 2.
226Zadanie 3.
226Ćwiczenie 1.
228Zadanie 1.
232Zadanie 5.
232Zadanie 6.
232Zadanie 7.
232Zadanie 1.
236Zadanie 2.
236Ćwiczenie 6.
240Zadanie 1.
240Zadanie 3.
241Zadanie 4.
241Zadanie 5.
241Zadanie 6.
241Zadanie 10.
241Zadanie 11.
241Zadanie 12.
241Zadanie 13.
241Ćwiczenie 2.
243Zadanie 1.
245Zadanie 2.
246Zadanie 3.
246Zadanie 4.
246Zadanie 5.
246Zadanie 6.
246Zadanie 7.
246Zadanie 8.
246Zadanie 3.
249Zadanie 7.
249Ćwiczenie 2.
251Zadanie 5.
253Zadanie 6.
253Zadanie 16.
254Zadanie 17.
254Zadanie 11.
260Zadanie 13.
260Zadanie 14.
260Zadanie 18.
260Zadanie 19.
260Zadanie 20.
260Zadanie 21.
260Zadanie 22.
261Zadanie 24.
261Zadanie 30.
261
