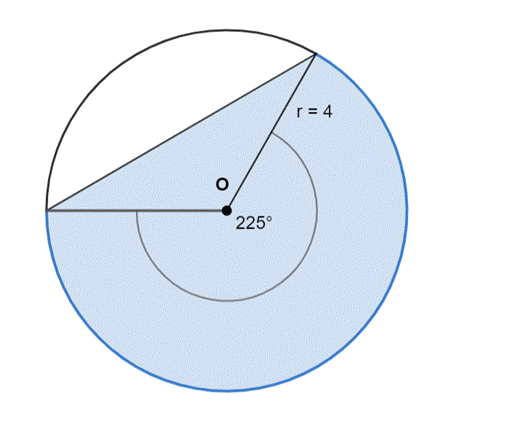
W tym zadaniu wyznacz pole odcinka koła oznaczonego na rysunku kolorem niebieskim.
Rysunek poglądowy:
Pt–pole trójkąta, Pw–pole wycinka, r–promień koła, α–kąt wycinka koła
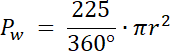
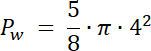
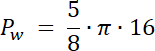
![]()
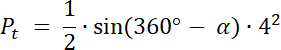
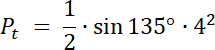
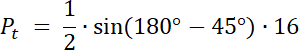
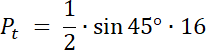
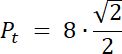
Pt = 4√2
PO = Pw + Pt
PO = Pw + Pt
PO = 10π–4√2
PO = 2(5π–√2)

W pierwszym kroku zauważ, że pole zamalowanego obszaru na niebiesko to suma pól: wycinka koła o kącie 225° i pola trójkąta równoramiennego o kącie między ramionami równym 135° i ramieniu o długości 3. Oblicz te pola i wyznacz ich sumę–otrzymany wynik to pole odcinka koła.

Ćwiczenie 1.
219Ćwiczenie 2.
221Zadanie 1.
222Zadanie 2.
222Zadanie 3.
222Ćwiczenie 1.
225Zadanie 1.
226Zadanie 2.
226Zadanie 3.
226Ćwiczenie 1.
228Zadanie 1.
232Zadanie 5.
232Zadanie 6.
232Zadanie 7.
232Zadanie 1.
236Zadanie 2.
236Ćwiczenie 6.
240Zadanie 1.
240Zadanie 3.
241Zadanie 4.
241Zadanie 5.
241Zadanie 6.
241Zadanie 10.
241Zadanie 11.
241Zadanie 12.
241Zadanie 13.
241Ćwiczenie 2.
243Zadanie 1.
245Zadanie 2.
246Zadanie 3.
246Zadanie 4.
246Zadanie 5.
246Zadanie 6.
246Zadanie 7.
246Zadanie 8.
246Zadanie 3.
249Zadanie 7.
249Ćwiczenie 2.
251Zadanie 5.
253Zadanie 6.
253Zadanie 16.
254Zadanie 17.
254Zadanie 11.
260Zadanie 13.
260Zadanie 14.
260Zadanie 18.
260Zadanie 19.
260Zadanie 20.
260Zadanie 21.
260Zadanie 22.
261Zadanie 24.
261Zadanie 30.
261
