W tym zadaniu musisz obliczyć pole figury zamalowanej na zielono.
Rysunek pomocniczy:
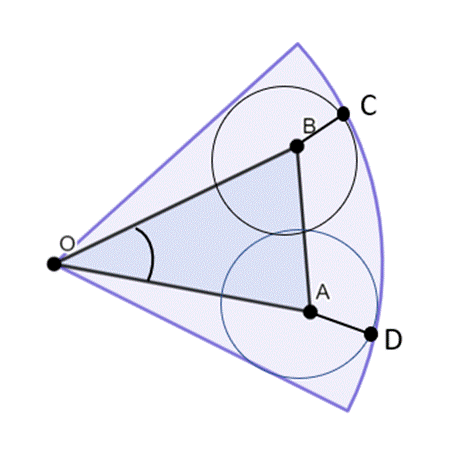
|OA| = |OB| = 6 cm
POAB = 9 cm
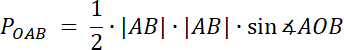
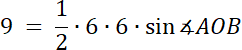
![]()
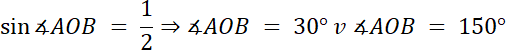
![]()
![]()
|∡O| = 2|∡AOB|
![]()
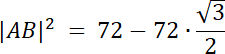
![]()
![]()
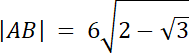
|AB| = 2r
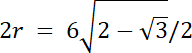
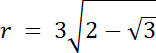
R = |OD|
r = |AD|
|OD| = |OA| + |AD
R = |OA| + |AD|
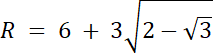
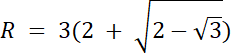
Rysunek pomocniczy 2:
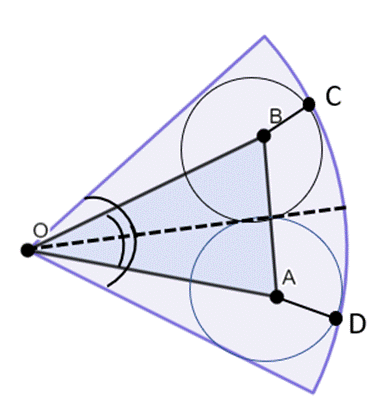
|∡O| = 2|∡AOB|
|∡O| = 60°
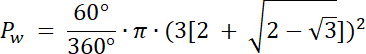
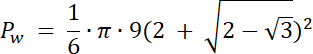
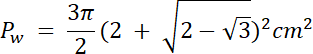

Na początku wyznacz kąt w trójkącie AOB, który leży naprzeciwko boku AB–wykorzystaj wzór na pole trójkąta z funkcją sinus. Następnie bok |AB| = 2r, gdzie r to długość promienia okręgu A oraz okręgu B. Kąt ∡O = 2|∡AOB|–z twierdzenia o kącie środkowym i wpisanym. Wyznacz na tej podstawie wartość promienia r. Zauważ, że promień wycinka okręgu jest równy |OD|, a |OD| = |OA| + |AD|, wyznacz z tego zapisu długość promienia R, a na koniec oblicz pole wycinka.

Ćwiczenie 1.
219Ćwiczenie 2.
221Zadanie 1.
222Zadanie 2.
222Zadanie 3.
222Ćwiczenie 1.
225Zadanie 1.
226Zadanie 2.
226Zadanie 3.
226Ćwiczenie 1.
228Zadanie 1.
232Zadanie 5.
232Zadanie 6.
232Zadanie 7.
232Zadanie 1.
236Zadanie 2.
236Ćwiczenie 6.
240Zadanie 1.
240Zadanie 3.
241Zadanie 4.
241Zadanie 5.
241Zadanie 6.
241Zadanie 10.
241Zadanie 11.
241Zadanie 12.
241Zadanie 13.
241Ćwiczenie 2.
243Zadanie 1.
245Zadanie 2.
246Zadanie 3.
246Zadanie 4.
246Zadanie 5.
246Zadanie 6.
246Zadanie 7.
246Zadanie 8.
246Zadanie 3.
249Zadanie 7.
249Ćwiczenie 2.
251Zadanie 5.
253Zadanie 6.
253Zadanie 16.
254Zadanie 17.
254Zadanie 11.
260Zadanie 13.
260Zadanie 14.
260Zadanie 18.
260Zadanie 19.
260Zadanie 20.
260Zadanie 21.
260Zadanie 22.
261Zadanie 24.
261Zadanie 30.
261
