W tym zadaniu musisz udowodnić tezę z treści zadania.
Rysunek pomocniczy:
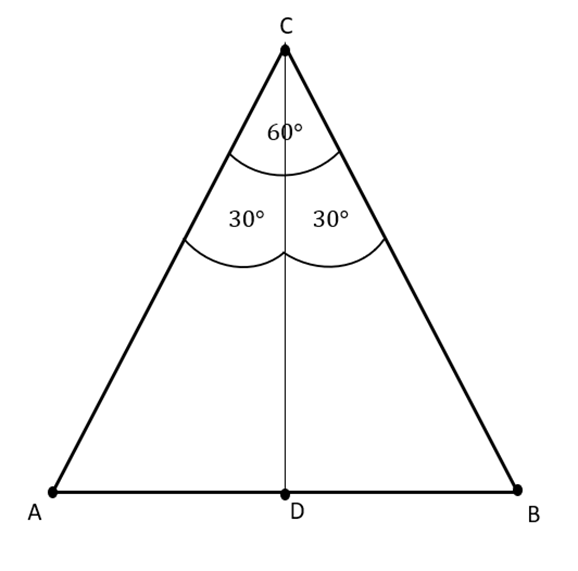
|AD| = x, |BD| = 2x

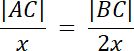
Przyjmij: |AC| = y
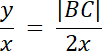
2xy = x∙|BC| / x
2y = |BC|
|AB| = |AD| + |DB|
|AB| = x + 2x
|AB| = 3x
![]()
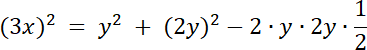
![]()
![]()
![]()
y = √3x
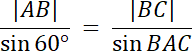
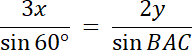
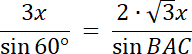
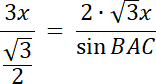
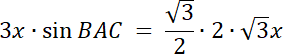
![]()
![]()
|∡BAC| = 90°

W pierwszym kroku wykorzystaj stosunek boku |AB| po podziale, który leży naprzeciw kąta C. Następnie, przyjmij długość dla boku |AC| i ze stosunku figur podobnych, wyznacz bok |BC|. Z twierdzenia cosinusów wyznacz zależność dla dwóch różnych boków, a na koniec z twierdzenia sinusów udowodnij tezę z treści zadania.

Ćwiczenie 1.
219Ćwiczenie 2.
221Zadanie 1.
222Zadanie 2.
222Zadanie 3.
222Ćwiczenie 1.
225Zadanie 1.
226Zadanie 2.
226Zadanie 3.
226Ćwiczenie 1.
228Zadanie 1.
232Zadanie 5.
232Zadanie 6.
232Zadanie 7.
232Zadanie 1.
236Zadanie 2.
236Ćwiczenie 6.
240Zadanie 1.
240Zadanie 3.
241Zadanie 4.
241Zadanie 5.
241Zadanie 6.
241Zadanie 10.
241Zadanie 11.
241Zadanie 12.
241Zadanie 13.
241Ćwiczenie 2.
243Zadanie 1.
245Zadanie 2.
246Zadanie 3.
246Zadanie 4.
246Zadanie 5.
246Zadanie 6.
246Zadanie 7.
246Zadanie 8.
246Zadanie 3.
249Zadanie 7.
249Ćwiczenie 2.
251Zadanie 5.
253Zadanie 6.
253Zadanie 16.
254Zadanie 17.
254Zadanie 11.
260Zadanie 13.
260Zadanie 14.
260Zadanie 18.
260Zadanie 19.
260Zadanie 20.
260Zadanie 21.
260Zadanie 22.
261Zadanie 24.
261Zadanie 30.
261
