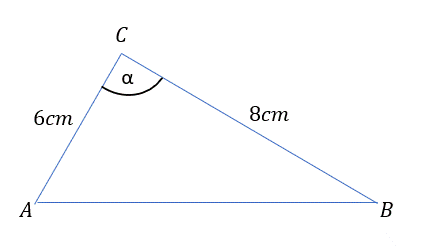
W tym zadaniu musisz wyznaczyć długość boku trójkąta, leżącego naprzeciwko kąta α, tak, aby trójkąt ten posiadał możliwe, największe pole.
Rysunek poglądowy:
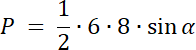
![]()
sin α = 1 wartość maksymalna dla α ⋲ (0°, 180°), więc:
Pmax = 24∙1 = 24 cm2
sin α = 1 dla α = 90°
62 + 82 = |AB|2
36 + 64 = |AB|2
|AB|2 = 100 |/√
|AB| = 10 cm

W tym zadaniu wyznacz pole trójkąta wykorzystując wzór z funkcją sinus. Następnie zauważ, że pole osiąga wartość maksymalną, kiedy funkcja sinus osiąga wartość maksymalną, czyli sin α = 1 dla α ⋲ (0°, 180°). Skoro kąt między bokami trójkąta jest równy 90°, to trójkąt ten jest prostokątny, więc z twierdzenia Pitagorasa wyznacz długość trzeciego boku.

Ćwiczenie 1.
219Ćwiczenie 2.
221Zadanie 1.
222Zadanie 2.
222Zadanie 3.
222Ćwiczenie 1.
225Zadanie 1.
226Zadanie 2.
226Zadanie 3.
226Ćwiczenie 1.
228Zadanie 1.
232Zadanie 5.
232Zadanie 6.
232Zadanie 7.
232Zadanie 1.
236Zadanie 2.
236Ćwiczenie 6.
240Zadanie 1.
240Zadanie 3.
241Zadanie 4.
241Zadanie 5.
241Zadanie 6.
241Zadanie 10.
241Zadanie 11.
241Zadanie 12.
241Zadanie 13.
241Ćwiczenie 2.
243Zadanie 1.
245Zadanie 2.
246Zadanie 3.
246Zadanie 4.
246Zadanie 5.
246Zadanie 6.
246Zadanie 7.
246Zadanie 8.
246Zadanie 3.
249Zadanie 7.
249Ćwiczenie 2.
251Zadanie 5.
253Zadanie 6.
253Zadanie 16.
254Zadanie 17.
254Zadanie 11.
260Zadanie 13.
260Zadanie 14.
260Zadanie 18.
260Zadanie 19.
260Zadanie 20.
260Zadanie 21.
260Zadanie 22.
261Zadanie 24.
261Zadanie 30.
261
