W tym zadaniu musisz obliczyć pole czworokąta, który znajduje się wewnątrz kwadratu ABCD.
Rysunek poglądowy:
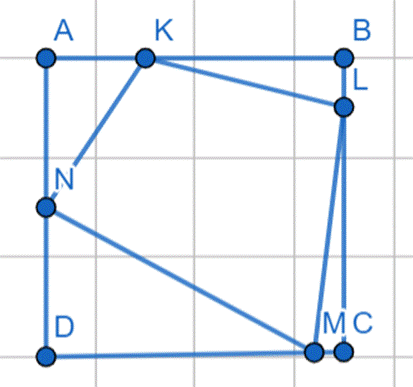
|AB| = |BC| = |CD| = |DA| = 12 cm:
Długości boków: |AK|, |KB|, |BL|, |LC|, |MC|, |MD|, |DN|, |NA|:
|AK| : |KB| = 1 : 2
2|AK| = |KB|
|AB| = |AK| + |KB|
|AB| = |AK| + 2|AK|
|AB| = 3|AK|
12 = 3|AK | /3
|AK| = 4 cm
|AK| = 4 cm, |KB| = 8 cm
|BL| : |LC| = 1 : 5
5|BL| = |LC|
|BC| = |BL| + |LC|
|BC| = |BL| + 5|BL|
|BC| = 6|BL|
12 = 6|BL | /6
|BL| = 2 cm
|BL| = 2 cm, |LC| = 10 cm
|DM| : |MC| = 7 : 5
![]()
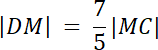
|CD| = |DM| + |MC|
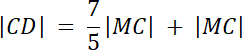
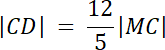
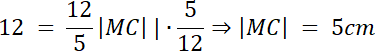
|MC| = 5 cm, |DM| = 7 cm
|DN| = |AN|
|DA| = |AN| + |DN|
|DA| = 2|AN|
12 = 2|AN| |/2
|AN| = 6 cm
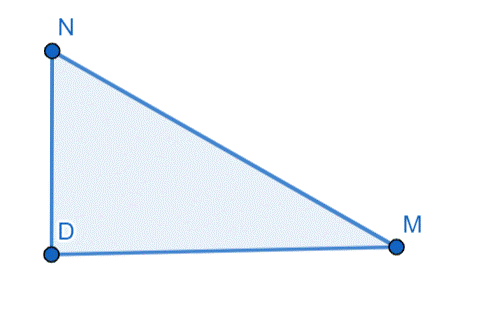
|AN| = 6 cm, |DN| = 6 cm
Pole Kwadratu ABCD = 122 = 144 cm2
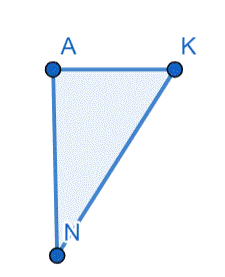
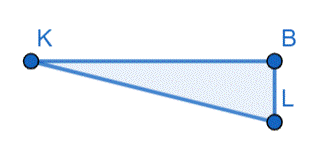
Pole Kwadratu ABCD = Pole Trójkąta AKN + Pole Trójkąta KBL + Pole Trójkąta LCM + Pole Trójkąta NDM + Pole Czworokąta KLMN
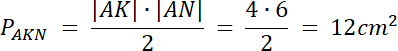
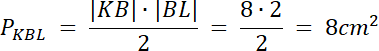

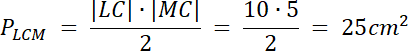
![]()
![]()
![]()
![]()

Najpierw narysuj kwadrat ABCD, oznacz na nim punkty K, L, M, N, a następnie wyznacz długości boków: |AK|, |KB|, |BL|, |LC|, |DM|, |MC|, |DN|, |AN|, korzystając z długości boku kwadratu ABCD i stosunku boków. Zauważ, że pole czworokąt KLMN to różnica między polem kwadratu ABCD a polami trójkątów prostokątnych: AKN, KBL, LCM, NDM, więc oblicz pole kwadratu i odejmij od niego pola czterech trójkątów, dzięki czemu otrzymasz pole czworokąta KLMN.

Ćwiczenie 1.
219Ćwiczenie 2.
221Zadanie 1.
222Zadanie 2.
222Zadanie 3.
222Ćwiczenie 1.
225Zadanie 1.
226Zadanie 2.
226Zadanie 3.
226Ćwiczenie 1.
228Zadanie 1.
232Zadanie 5.
232Zadanie 6.
232Zadanie 7.
232Zadanie 1.
236Zadanie 2.
236Ćwiczenie 6.
240Zadanie 1.
240Zadanie 3.
241Zadanie 4.
241Zadanie 5.
241Zadanie 6.
241Zadanie 10.
241Zadanie 11.
241Zadanie 12.
241Zadanie 13.
241Ćwiczenie 2.
243Zadanie 1.
245Zadanie 2.
246Zadanie 3.
246Zadanie 4.
246Zadanie 5.
246Zadanie 6.
246Zadanie 7.
246Zadanie 8.
246Zadanie 3.
249Zadanie 7.
249Ćwiczenie 2.
251Zadanie 5.
253Zadanie 6.
253Zadanie 16.
254Zadanie 17.
254Zadanie 11.
260Zadanie 13.
260Zadanie 14.
260Zadanie 18.
260Zadanie 19.
260Zadanie 20.
260Zadanie 21.
260Zadanie 22.
261Zadanie 24.
261Zadanie 30.
261
