W tym zadaniu musisz obliczyć pole figury zamalowanej na zielono.
Rysunek pomocniczy:
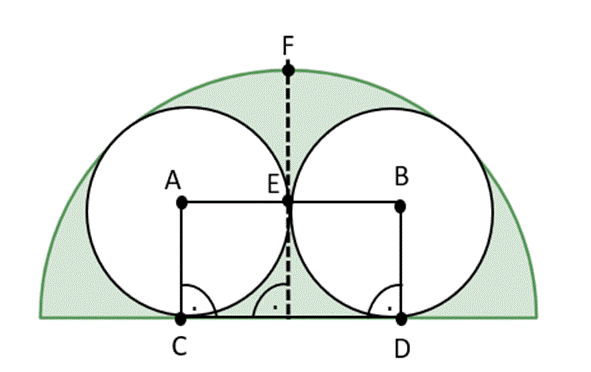
|AE| = ra, |EB| = rb
|AC| = ra, |BD| = rb
|AC| = |BD|⇒ ra = rb
PCDBA = |AC|∙|AB|
PCDBA = ra∙(ra + rb)
PCDBA = ra∙2ra
PCDBA = 2ra2 i PCDBA = 8
2ra2 = 8 /2
ra2 = 4 /√
ra = 2
|AB| = |CD| = 4
|AC| = |BD| = 2
Rysunek pomocniczy 2:
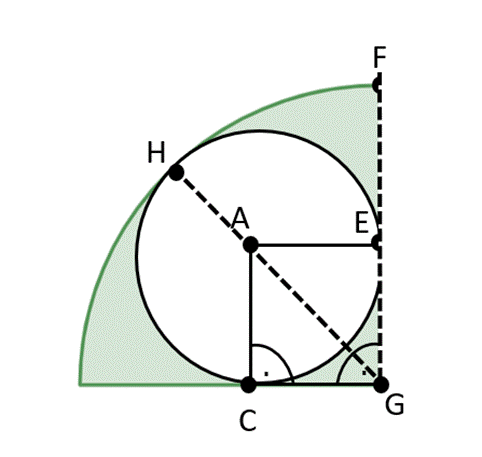
|CA| = |AE| = r = 2
|AG| = R–r
|AG| = R–2
|CA|2 + |AE|2 = |AG|2
22 + 22 = |AG|2
|AG|2 = 8 /√
|AG| = 2√2
R–2 = 2√2 | + 2
R = 2√2 + 2
Pp–pole zielonego półkola
Pwa–pole wycinka kołowego o środku a
Pwb–pole wycinka kołowego o środku b
PCDBA–pole prostokąta
Pwa = Pwb
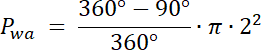
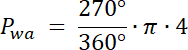
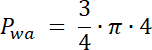
![]()
![]()
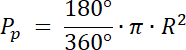
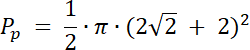
![]()
![]()
![]()
Pf–pole zielonej figury:
Pf = Pp–Pwa–Pwb–PCDBA
![]()
![]()
![]()

Na początku wyznacz promienie kół A i B, a w następnym kroku wyznacz promień półkola. W tym celu narysuj trójkąt ACG i określ, jego boki. Długość |AG| wyznacz z twierdzenia Pitagorasa, dzięki temu wyznaczysz promień półkola. Na koniec, pole figury zamalowanej na zielono to różnica: półkola, dwóch wycinków okręgów o środkach A i B (każdy z tych wycinków ma kąt równy 270°), pola prostokąta.

Ćwiczenie 1.
219Ćwiczenie 2.
221Zadanie 1.
222Zadanie 2.
222Zadanie 3.
222Ćwiczenie 1.
225Zadanie 1.
226Zadanie 2.
226Zadanie 3.
226Ćwiczenie 1.
228Zadanie 1.
232Zadanie 5.
232Zadanie 6.
232Zadanie 7.
232Zadanie 1.
236Zadanie 2.
236Ćwiczenie 6.
240Zadanie 1.
240Zadanie 3.
241Zadanie 4.
241Zadanie 5.
241Zadanie 6.
241Zadanie 10.
241Zadanie 11.
241Zadanie 12.
241Zadanie 13.
241Ćwiczenie 2.
243Zadanie 1.
245Zadanie 2.
246Zadanie 3.
246Zadanie 4.
246Zadanie 5.
246Zadanie 6.
246Zadanie 7.
246Zadanie 8.
246Zadanie 3.
249Zadanie 7.
249Ćwiczenie 2.
251Zadanie 5.
253Zadanie 6.
253Zadanie 16.
254Zadanie 17.
254Zadanie 11.
260Zadanie 13.
260Zadanie 14.
260Zadanie 18.
260Zadanie 19.
260Zadanie 20.
260Zadanie 21.
260Zadanie 22.
261Zadanie 24.
261Zadanie 30.
261
