W tym zadaniu musisz wyznaczyć promień okręgu, który jest opisany na trójkącie ABC.
Rysunek poglądowy:
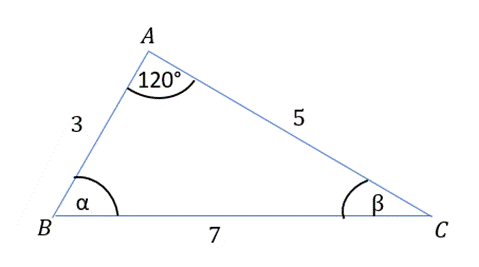
Przyjmij, że:
|∡ABC| = α i |∡BCA| = β
α + β + 120° = 180° |–120°
α + β = 60°
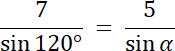
![]()
![]()
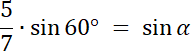

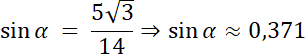
![]()
α + β = 60°|–α
β = 60°–α⇒ γ ≈ 60°–22°
γ ≈ 38°⇒ |∡BCA| ≈ 38°

W pierwszym kroku narysuj trójkąt ABC, zaznacz na nim długość boków trójkąta ABC, kąt |∡BAC|. Długość boków |AB| i |BC| przepisz z podpunktu a, tego zadania. Następnie wykorzystaj zależność na sumę kątów w trójkącie, aby wyznaczyć sumę niewiadomych kątów. Korzystając z twierdzenia sinusów–oblicz przybliżoną wartość kąta |∡ABC|, a następnie wyznacz miarę kąta |∡BCA|.

Ćwiczenie 1.
219Ćwiczenie 2.
221Zadanie 1.
222Zadanie 2.
222Zadanie 3.
222Ćwiczenie 1.
225Zadanie 1.
226Zadanie 2.
226Zadanie 3.
226Ćwiczenie 1.
228Zadanie 1.
232Zadanie 5.
232Zadanie 6.
232Zadanie 7.
232Zadanie 1.
236Zadanie 2.
236Ćwiczenie 6.
240Zadanie 1.
240Zadanie 3.
241Zadanie 4.
241Zadanie 5.
241Zadanie 6.
241Zadanie 10.
241Zadanie 11.
241Zadanie 12.
241Zadanie 13.
241Ćwiczenie 2.
243Zadanie 1.
245Zadanie 2.
246Zadanie 3.
246Zadanie 4.
246Zadanie 5.
246Zadanie 6.
246Zadanie 7.
246Zadanie 8.
246Zadanie 3.
249Zadanie 7.
249Ćwiczenie 2.
251Zadanie 5.
253Zadanie 6.
253Zadanie 16.
254Zadanie 17.
254Zadanie 11.
260Zadanie 13.
260Zadanie 14.
260Zadanie 18.
260Zadanie 19.
260Zadanie 20.
260Zadanie 21.
260Zadanie 22.
261Zadanie 24.
261Zadanie 30.
261
