W tym zadaniu musisz wykazać, że trzy przecinające się środkowe w trójkącie, wyznaczają sześć trójkątów, gdzie każdy z nich ma równe pole.
Rysunek poglądowy:
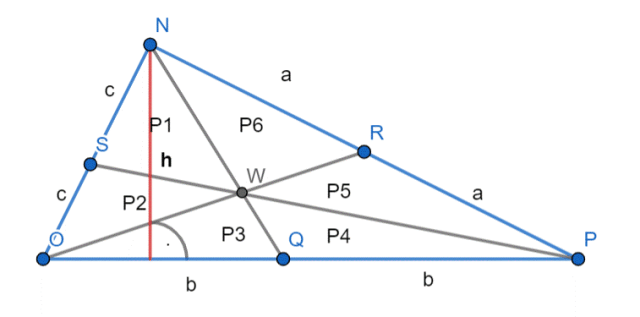
Trójkąty NOQ i NQP posiadają równe pola, ponieważ mają taką samą wysokość i ich podstawy są sobie równe, więc:
PNOQ = PNQP, więc:
P1 + P2 + P3 = P4 + P5 + P6
Trójkąty: WOQ i WQP, NSW i SWO, NWR i RPW mają równe pola, ponieważ posiadają podstawy i wysokości tej samej długości, więc:
P1 = P2, P3 = P4, P5 = P6,
2∙P2 + P3 = P4 + 2∙P5⇒ P3 = P4, więc:
2∙P2 + P4 = P4 + 2∙P5 |–P4
2∙P2 = 2∙P5 |/2
P2 = P5⇒ P2 = P6,⇒ P2 = P5 = P6 = P1, więc:
Trójkąty SOP i ROP mają pola tej samej długości, bo posiadają taką sama wysokość oraz długość podstawy, więc:
P2 + P3 + P4 = P3 + P4 + P5 dla P3 = P4
P2 + 2P3 = 2P3 + P5 , więc P3 = P5 = P2 = P4,
Ostatecznie P1 = P2 = P3 = P4 = P5 = P6

Narysuj trójkąt, wyprowadź trzy środkowe w nim, udowodnij twierdzenie, wykorzystując informację o długości podstaw tych trójkątów oraz ich wysokościach.

Ćwiczenie 1.
219Ćwiczenie 2.
221Zadanie 1.
222Zadanie 2.
222Zadanie 3.
222Ćwiczenie 1.
225Zadanie 1.
226Zadanie 2.
226Zadanie 3.
226Ćwiczenie 1.
228Zadanie 1.
232Zadanie 5.
232Zadanie 6.
232Zadanie 7.
232Zadanie 1.
236Zadanie 2.
236Ćwiczenie 6.
240Zadanie 1.
240Zadanie 3.
241Zadanie 4.
241Zadanie 5.
241Zadanie 6.
241Zadanie 10.
241Zadanie 11.
241Zadanie 12.
241Zadanie 13.
241Ćwiczenie 2.
243Zadanie 1.
245Zadanie 2.
246Zadanie 3.
246Zadanie 4.
246Zadanie 5.
246Zadanie 6.
246Zadanie 7.
246Zadanie 8.
246Zadanie 3.
249Zadanie 7.
249Ćwiczenie 2.
251Zadanie 5.
253Zadanie 6.
253Zadanie 16.
254Zadanie 17.
254Zadanie 11.
260Zadanie 13.
260Zadanie 14.
260Zadanie 18.
260Zadanie 19.
260Zadanie 20.
260Zadanie 21.
260Zadanie 22.
261Zadanie 24.
261Zadanie 30.
261
