W tym zadaniu musisz udowodnić, że pola trójkątów AOD i BCO są równe √P1∙P2.
Rysunek pomocniczy:
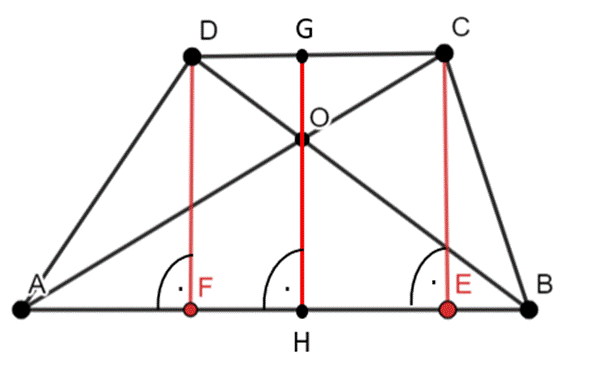
PDOC = P1
PABO = P2
Trójkąty DOC i ABO są podobne–mają te same wartości kątów
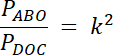
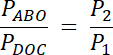
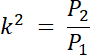
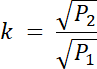
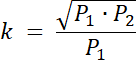
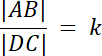
|AB| = k∙|DC|
Przyjmij: h–wysokość trapezu
h = |GH| i |GH| = |GO| + |OH|
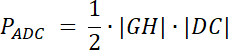
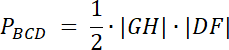
![]()
![]()
![]()
![]()
![]()
![]()
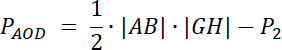
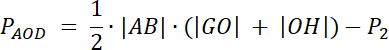
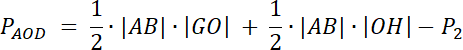
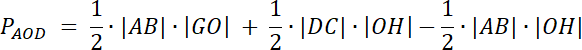
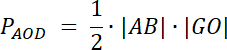
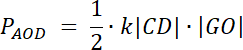
![]()
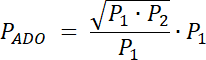
![]()

Na początku, wykorzystaj twierdzenie na stosunek pól figur podobnych. W następnym kroku zauważ, że trójkąty ABC i ABD mają równe pola, dzięki temu możesz udowodnić, że pola trójkątów AOD i BCO są sobie równe. Na koniec, zapisz wzór na pole AOD, uwzględniając stosunek pól figur.

Ćwiczenie 1.
219Ćwiczenie 2.
221Zadanie 1.
222Zadanie 2.
222Zadanie 3.
222Ćwiczenie 1.
225Zadanie 1.
226Zadanie 2.
226Zadanie 3.
226Ćwiczenie 1.
228Zadanie 1.
232Zadanie 5.
232Zadanie 6.
232Zadanie 7.
232Zadanie 1.
236Zadanie 2.
236Ćwiczenie 6.
240Zadanie 1.
240Zadanie 3.
241Zadanie 4.
241Zadanie 5.
241Zadanie 6.
241Zadanie 10.
241Zadanie 11.
241Zadanie 12.
241Zadanie 13.
241Ćwiczenie 2.
243Zadanie 1.
245Zadanie 2.
246Zadanie 3.
246Zadanie 4.
246Zadanie 5.
246Zadanie 6.
246Zadanie 7.
246Zadanie 8.
246Zadanie 3.
249Zadanie 7.
249Ćwiczenie 2.
251Zadanie 5.
253Zadanie 6.
253Zadanie 16.
254Zadanie 17.
254Zadanie 11.
260Zadanie 13.
260Zadanie 14.
260Zadanie 18.
260Zadanie 19.
260Zadanie 20.
260Zadanie 21.
260Zadanie 22.
261Zadanie 24.
261Zadanie 30.
261
