W tym zadaniu musisz obliczyć pole koła
a–bok ramienia–4 cm
R–promień okręgu opisanego na trójkącie
α, β, γ–kąty w trójkącie
Kąt między ramionami = 120°
α + β + γ = 180° |–120°
β + γ = 60°–trójkąt równoramienny, więc
β = γ⇒ β = 30° i γ = 30°
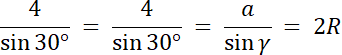
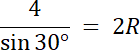
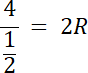
8 = 2R/ 2
R = 4
![]()
![]()

W tym zadaniu wyznacz jaki kąt leży, naprzeciwko ramienia trójkąta równoramiennego, wyznacz promień okręgu opisanego na trójkącie z twierdzenia sinusów, a następnie oblicz pole tego koła.

Ćwiczenie 1.
219Ćwiczenie 2.
221Zadanie 1.
222Zadanie 2.
222Zadanie 3.
222Ćwiczenie 1.
225Zadanie 1.
226Zadanie 2.
226Zadanie 3.
226Ćwiczenie 1.
228Zadanie 1.
232Zadanie 5.
232Zadanie 6.
232Zadanie 7.
232Zadanie 1.
236Zadanie 2.
236Ćwiczenie 6.
240Zadanie 1.
240Zadanie 3.
241Zadanie 4.
241Zadanie 5.
241Zadanie 6.
241Zadanie 10.
241Zadanie 11.
241Zadanie 12.
241Zadanie 13.
241Ćwiczenie 2.
243Zadanie 1.
245Zadanie 2.
246Zadanie 3.
246Zadanie 4.
246Zadanie 5.
246Zadanie 6.
246Zadanie 7.
246Zadanie 8.
246Zadanie 3.
249Zadanie 7.
249Ćwiczenie 2.
251Zadanie 5.
253Zadanie 6.
253Zadanie 16.
254Zadanie 17.
254Zadanie 11.
260Zadanie 13.
260Zadanie 14.
260Zadanie 18.
260Zadanie 19.
260Zadanie 20.
260Zadanie 21.
260Zadanie 22.
261Zadanie 24.
261Zadanie 30.
261
