Dany jest czworokąt
. Trzy jego boki są równej długości. Wiedząc, że czwarty ma długość równą każdej z przekątnych, oblicz miary kątów wewnętrznych tego czworokąta.
Załóżmy, że
. Wtedy
.
Wiemy, że trójkąt
jest równoramienny. Oznaczmy miarę kąta
jako
.
Oznacza to, że miary kątów:
są równe:
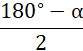
Z pierwszego założenia wynika, że
są przystające z zasady bok-bok-bok. Mamy więc:
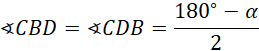
Na kąt
składa się kąt
oraz
:
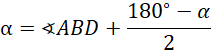
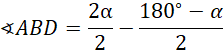
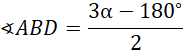
Trójkąt
jest równoramienny, więc:
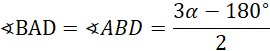
Z pierwszego założenia wynika, że
są przystające z zasady bok-bok-bok. Mamy więc:
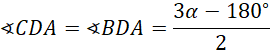
Suma kątów wewnętrznych w czworokącie wypukłym jest równa
, czyli:
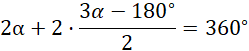
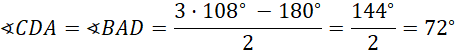
Odp.
.
Wykorzystujemy relacje między kątami wewnętrznymi trójkątów równoramiennych, przystawanie figur oraz sumę kątów wewnętrznych czworokąta wypukłego.