Udowodnij, że suma kątów w czworokącie wypukłym jest równa
.
Założenia:
Teza:
Suma kątów w czworokącie wypukłym jest równa
.
Dowód:
Tworzymy prostą
przechodzącą przez punkt A w taki sposób, że
. Kąty
są naprzemianległe do kątów przy prostej
. Razem tworzą kąt półpełny, czyli
.
W analogiczny sposób rozumujemy z kątami
, tym razem tworząc prostą
przechodzącą przez punkt C oraz
.
Mamy zatem układ:
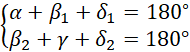
Dodajemy stronami:
Czyli suma kątów w czworokącie jest równa
.
(co kończy dowód)
Wykorzystujemy argument użyty do dowodu, że suma kątów w trójkącie jest równa
oraz fakt, że każdy
-kąt wypukły daje się podzielić na
trójkątów.