Teza:
Dwusieczne kątów przy jednym boku są prostopadłe.
Dowód:
Niech dane będą kąty
![]() , oparte na wspólnym boku. Niech
, oparte na wspólnym boku. Niech
![]() będzie kątem utworzonym na przecięciu dwusiecznych. Wiemy, że suma kątów opartych na jednym boku jest równa
będzie kątem utworzonym na przecięciu dwusiecznych. Wiemy, że suma kątów opartych na jednym boku jest równa
![]() :
:
![]()
Dzielimy obustronnie przez dwa:
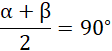
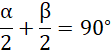
Zauważamy, że lewa strona to suma kątów wyznaczonych przez dwusieczną. Suma kątów wewnętrznych trójkąta wyznaczonego przez przecięte dwusieczne:
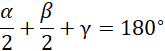
czyli:
![]()
Dwusieczne kątów przecinają się pod kątem prostym.
![]() (co kończy dowód)
(co kończy dowód)

Wykorzystujemy zależności między kątami wewnętrznymi równoległoboku, między kątami podzielonymi przez dwusieczną oraz sumę kątów wewnętrznych trójkąta.