Dane są trójkąty
. Poprowadzono środkowe, odpowiednio
i
. Wiadomo, że
i
. Udowodnij, że trójkąty
oraz
są przystające.
Teza:
Trójkąty
oraz
są przystające.
Dowód:
Zaznaczmy w trójkącie
punkt
taki, że
a w trójkącie punkt
taki, że
.
Tworzymy odcinki
i
(linie środkowe).
Wykorzystujemy twierdzenie o linii środkowej w trójkącie:
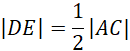
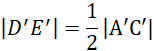
Skoro
, to znaczy, że
.
Skoro
, to:
.
Trójki:
i
spełniają zasadę przystawania trójkątów bok-bok-bok, czyli trójkąty
i
są przystające.
Skoro trójkąty
i
są przystające, to znaczy, że kąty
i
są sobie równe.
Trójki:
i
spełniają zasadę przystawania trójkątów bok-kąt-bok, czyli trójkąty
i
są przystające.
Skoro trójkąty
i
są przystające, to znaczy, że boki
i
są sobie równe.
Punkt
dzieli bok
w taki sposób, że
a
dzieli
w taki sposób, że
. Wraz z powyższym mamy, że:
Trójki:
i
spełniają zasadę przystawania trójkątów bok-bok-bok, czyli trójkąty
oraz
są przystające.
(co kończy dowód)
Wykorzystujemy zasady przystawania trójkątów:
bok-bok-bok: trzy boki trójkątów są odpowiednio równe, oraz
bok-kąt-bok: dwa boki i kąt między nimi zawarty są odpowiednio równe.
Linia środkowa to linia łącząca środki dwóch boków trójkąta. Linia ta jest równoległa do odpowiadającego boku oraz ma połowę jego długości.