Wyznacz objętość (z dokładnością do 1 dm3) i pole powierzchni całkowitej (z dokładnością do 1 dm2) tego graniastosłupa, jeśli krawędź podstawy graniastosłupa prawidłowego trójkątnego ma długość 4,2 dm. Wierzchołek górnej podstawy połączono ze środkami krawędzi dolnej podstawy odcinkami zawartymi w sąsiednich ścianach bocznych. Odcinki te tworzą kąt .
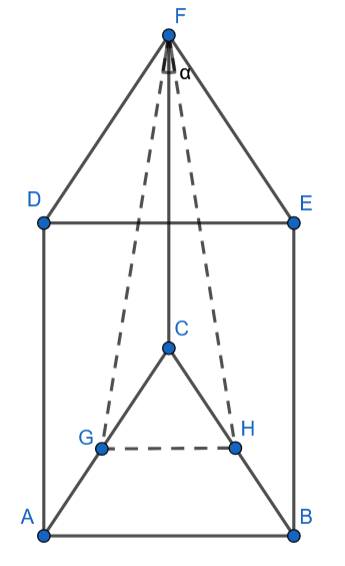 - wysokość graniastosłupa
- wysokość graniastosłupa
Trójkąty ABC i GHC są podobne z cechy KKK, więc trójkąt GHC jest również równoboczny.

Skorzystaj z twierdzenia cosinusów, aby obliczyć długości odcinków GF i HF, a następnie z twierdzenia Pitagorasa wyznacz długość wysokość graniastosłupa oraz jego objętość i pole całkowite.

Zadanie 1.10.
19Zadanie 1.12.
19Zadanie 1.13.
19Zadanie 2.
20Zadanie 2.4.
27Zadanie 2.8.
27Zadanie 2.11.
28Zadanie 2.12.
28Zadanie 2.14.
28Zadanie 2.15.
29Zadanie 2.16.
29Zadanie 2.17.
29Zadanie 2.18.
29Zadanie 3.4.
34Zadanie 3.5.
34Zadanie 3.6.
35Zadanie 2.
36Zadanie 4.4.
46Zadanie 4.6.
46Zadanie 4.9.
46Zadanie 4.10.
46Zadanie 4.14.
47Zadanie 4.17.
47Zadanie 4.20.
47Zadanie 5.4.
61Zadanie 5.5.
61Zadanie 5.6.
61Zadanie 5.9.
61Zadanie 5.13.
61Zadanie 5.21.
62Zadanie 5.29.
63Zadanie 6.5.
73Zadanie 6.6.
73Zadanie 6.7.
73Zadanie 6.10.
74Zadanie 6.14.
74Zadanie 6.15.
74Zadanie 7.13.
93Zadanie 38.
108Zadanie 56.
110
