Oblicz tangens kąta nachylenia tej płaszczyzny do płaszczyzny podstawy ostrosłupa, jeśli w ostrosłupie prawidłowym czworokątnym kąty płaskie przy wierzchołku są równe . Przez środki dwóch sąsiednich krawędzi podstawy i wierzchołek ostrosłupa poprowadzono płaszczyznę.
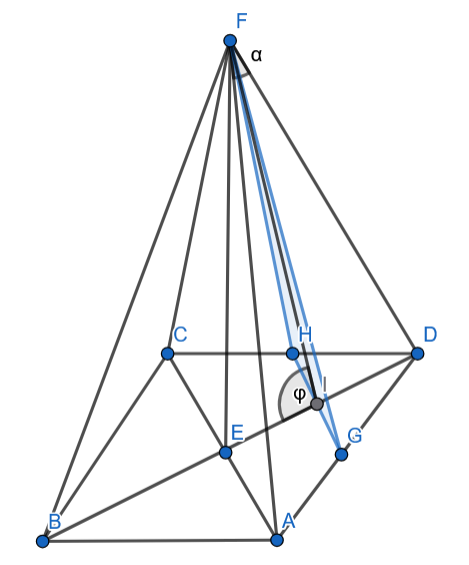 – krawędź podstawy – wysokość ostrosłupa – krawędź boczna
– krawędź podstawy – wysokość ostrosłupa – krawędź boczna

Dwukrotnie skorzystaj z twierdzenia Pitagorasa, aby obliczyć długości odcinków GH, IE oraz wysokości ostrosłupa oraz z funkcji sinus wyznacz długość krawędzi bocznej, a następnie tangens podanego kąta.

Zadanie 1.10.
19Zadanie 1.12.
19Zadanie 1.13.
19Zadanie 2.
20Zadanie 2.4.
27Zadanie 2.8.
27Zadanie 2.11.
28Zadanie 2.12.
28Zadanie 2.14.
28Zadanie 2.15.
29Zadanie 2.16.
29Zadanie 2.17.
29Zadanie 2.18.
29Zadanie 3.4.
34Zadanie 3.5.
34Zadanie 3.6.
35Zadanie 2.
36Zadanie 4.4.
46Zadanie 4.6.
46Zadanie 4.9.
46Zadanie 4.10.
46Zadanie 4.14.
47Zadanie 4.17.
47Zadanie 4.20.
47Zadanie 5.4.
61Zadanie 5.5.
61Zadanie 5.6.
61Zadanie 5.9.
61Zadanie 5.13.
61Zadanie 5.21.
62Zadanie 5.29.
63Zadanie 6.5.
73Zadanie 6.6.
73Zadanie 6.7.
73Zadanie 6.10.
74Zadanie 6.14.
74Zadanie 6.15.
74Zadanie 7.13.
93Zadanie 38.
108Zadanie 56.
110
