Oblicz wymiary prostopadłościanu o największej objętości, jeśli w stożek o promieniu podstawy R i wysokości H wpisano prostopadłościan, w którym stosunek krawędzi podstawy jest równy 2.
– boki prostokąta – przekątna prostokąta – wysokość prostopadlościanu
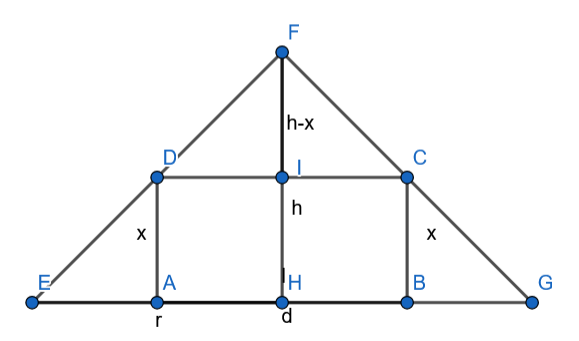
Trójkąty EGF i DCF są podobne z cechy KKK.

Skorzystaj z twierdzenia Pitagorasa i wyznacz przekątną prostokąta. Następnie zauważ, że trójkąty przedstawione na rysunku są podobne. Na tej podstawie zapisz stosunek długości ich krótszych podstaw oraz przeciwprostokątnych i na tej podstawie wyznacz długość i określ dziedzinę – wysokość i bok muszą być dodatnie. Następie oblicz jego objętość – zauważ, że powstanie funkcja zmiennej , oblicz jej pochodną i miejsce zerowe. Na koniec dla wyznaczonej długości boku wyznacz pozostałe wymiary prostopadłościanu.

Zadanie 1.10.
19Zadanie 1.12.
19Zadanie 1.13.
19Zadanie 2.
20Zadanie 2.4.
27Zadanie 2.8.
27Zadanie 2.11.
28Zadanie 2.12.
28Zadanie 2.14.
28Zadanie 2.15.
29Zadanie 2.16.
29Zadanie 2.17.
29Zadanie 2.18.
29Zadanie 3.4.
34Zadanie 3.5.
34Zadanie 3.6.
35Zadanie 2.
36Zadanie 4.4.
46Zadanie 4.6.
46Zadanie 4.9.
46Zadanie 4.10.
46Zadanie 4.14.
47Zadanie 4.17.
47Zadanie 4.20.
47Zadanie 5.4.
61Zadanie 5.5.
61Zadanie 5.6.
61Zadanie 5.9.
61Zadanie 5.13.
61Zadanie 5.21.
62Zadanie 5.29.
63Zadanie 6.5.
73Zadanie 6.6.
73Zadanie 6.7.
73Zadanie 6.10.
74Zadanie 6.14.
74Zadanie 6.15.
74Zadanie 7.13.
93Zadanie 38.
108Zadanie 56.
110
