Oblicz pole powierzchni bocznej ostrosłupa, jeśli w kulę o promieniu R wpisano ostrosłup prawidłowy czworokątny. Kąt płaski przy wierzchołku tego ostrosłupa ma miarę .
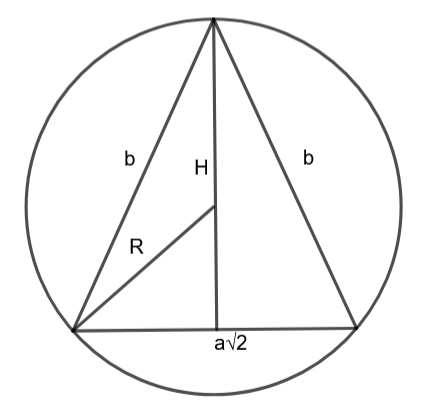 – krawędź podstawy ostrosłupa - wysokość ściany bocznej
– krawędź podstawy ostrosłupa - wysokość ściany bocznej

Zauważ, że połowa krawędzi podstawy, wysokość ściany bocznej i krawędź boczna ostrosłupa tworzą trójkąt prostokątny. Skorzystaj z funkcji sinus, cosinus oraz twierdzenia Pitagorasa, aby wyznaczyć wysokość bryły. Następnie zauważ, że połowa przekątnej podstawy, różnica wysokości i promienia kuli oraz promień kuli tworzą trójkąt prostokątny – wyznacz długość krawędzi bocznej z powstałego równania. Na koniec oblicz pole boczne bryły.

Zadanie 1.10.
19Zadanie 1.12.
19Zadanie 1.13.
19Zadanie 2.
20Zadanie 2.4.
27Zadanie 2.8.
27Zadanie 2.11.
28Zadanie 2.12.
28Zadanie 2.14.
28Zadanie 2.15.
29Zadanie 2.16.
29Zadanie 2.17.
29Zadanie 2.18.
29Zadanie 3.4.
34Zadanie 3.5.
34Zadanie 3.6.
35Zadanie 2.
36Zadanie 4.4.
46Zadanie 4.6.
46Zadanie 4.9.
46Zadanie 4.10.
46Zadanie 4.14.
47Zadanie 4.17.
47Zadanie 4.20.
47Zadanie 5.4.
61Zadanie 5.5.
61Zadanie 5.6.
61Zadanie 5.9.
61Zadanie 5.13.
61Zadanie 5.21.
62Zadanie 5.29.
63Zadanie 6.5.
73Zadanie 6.6.
73Zadanie 6.7.
73Zadanie 6.10.
74Zadanie 6.14.
74Zadanie 6.15.
74Zadanie 7.13.
93Zadanie 38.
108Zadanie 56.
110
