Prosto do matury 4. Zakres podstawowy i rozszerzony. Podręcznik - rozwiązania i odpowiedzi

Podręcznik, Wydawnictwo: Nowa Era

Zadanie 8.11. - strona 102

Wyznacz stosunek objętości ostrosłupa do objętości kuli, jeśli na kuli opisano ostrosłup prawidłowy czworokątny o najmniejszej objętości.

$r$ – promień kuli $a$ – krawędź podstawy $h$ - wysokość ostrosłupa ${| EB |}^{2} + r^{2} = {(h - r)}^{2}$ $| EB | = \sqrt{h^{2} - 2 h r}$

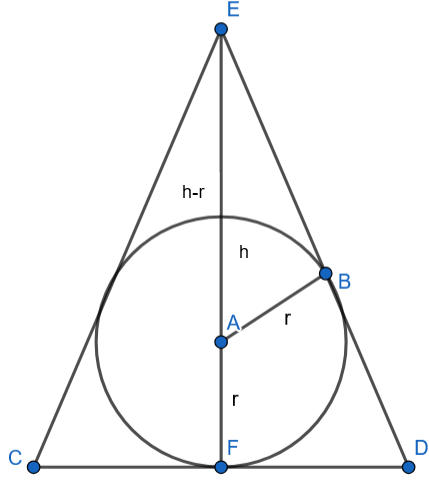
Trójkąty ABE i DEF są podobne z cechy KKK

$\frac{\sqrt{h^{2} - 2 h r}}{r} = \frac{h}{\frac{a}{2}}$ $a = \frac{2 h r}{\sqrt{h^{2} - 2 h r}}$ $\frac{2 h r}{\sqrt{h^{2} - 2 h r}} > 0$ $h > 0$ $V (h) = \frac{1}{3} \cdot a^{2} \cdot h = \frac{1}{3} \cdot \frac{4 h^{2} r^{2}}{(h^{2} - 2 h r)} \cdot h = \frac{4}{3} \cdot \frac{h^{2} r^{2}}{h - 2 r}$ $V^{'} (h) = \frac{2 h r^{2} (h - 2 r) - h^{2} r^{2}}{{(h - 2 r)}^{2}} = \frac{h^{2} r^{2} - 4 h r^{3}}{{(h - 2 r)}^{2}}$ $\frac{h^{2} r^{2} - 4 h r^{3}}{{(h - 2 r)}^{2}}$ $h r^{2} (h - 4 r) = 0$ $h = 4 r$ $V_{S} = \frac{4}{3} \cdot \frac{16 r^{2} \cdot r^{2}}{4 r - 2 r} = \frac{32 r^{3}}{3}$ $V_{K} = \frac{4}{3} π r^{3}$ $\frac{V_{S}}{V_{K}} = \frac{\frac{32 r^{3}}{3}}{\frac{4}{3} π r^{3}} = \frac{8}{π}$

Skorzystaj z twierdzenia Pitagorasa, aby wyznaczyć długość odcinka EB. Następnie zauważ, że trójkąty przedstawione na rysunku są podobne. Na tej podstawie zapisz stosunek długości odpowiadających sobie boków i na tej podstawie wyznacz długość $h$ i określ dziedzinę – wysokość i promień muszą być dodatnie. Następie oblicz jego objętość – zauważ, że powstanie funkcja zmiennej $h$ , oblicz jej pochodną i miejsce zerowe. A następnie objętość stożka i kuli dla wyznaczonej długości $h$ oraz ich stosunek.

Zadanie 10, strona 112, Matematyka wokół nas. Klasa 6. Podręcznik – rozwiązania i odpowiedzi

Zadanie 4., strona 257, Matematyka wokół nas. Klasa 8. Podręcznik - rozwiązania i odpowiedzi

Zadanie 8, strona 203, Matematyka z kluczem. Klasa 8. Podręcznik - rozwiązania i odpowiedzi

Zadanie 16., strona 118, Matematyka. Klasa 7. Podręcznik – rozwiązania i odpowiedzi

Zadanie 3, strona 24, Matematyka. Klasa 6. Zeszyt ćwiczeń – rozwiązania i odpowiedzi

Zadanie 12, strona 6, Matura z matematyki. Arkusz próbny. Poziom podstawowy. Kwiecień 2020

Zadanie 5.57, strona 110, Matematyka 4. Zakres podstawowy. Zbiór zadań - rozwiązania i odpowiedzi

Ćwiczenie 2, strona 170, Matematyka. Klasa 1. Podręcznik. Zakres rozszerzony. Część 1 – rozwiązania i odpowiedzi

Zadanie 28, strona 47, Matematyka z kluczem. Klasa 6. Zbiór zadań - rozwiązania i odpowiedzi

Zadanie 4, strona 73, Matematyka. Klasa 5. Zeszyt ćwiczeń – rozwiązania i odpowiedzi

17

17

17

18

18

18

18

18

18

Zadanie 1.10.

19

19

19

19

Zadanie 1.12.

19

19

19

19

19

19

Zadanie 1.13.

19

19

19

19

19

19

19

19

19

20

20

20

20

Zadanie 2.

20

20

20

20

20

20

20

20

20

27

27

27

Zadanie 2.4.

27

27

27

27

27

27

27

27

Zadanie 2.8.

27

27

27

27

27

28

28

Zadanie 2.11.

28

28

28

28

28

28

Zadanie 2.12.

28

28

28

28

Zadanie 2.14.

28

28

28

28

28

Zadanie 2.15.

29

29

29

29

29

29

Zadanie 2.16.

29

29

29

29

29

Zadanie 2.17.

29

29

29

29

29

Zadanie 2.18.

29

29

29

29

30

30

30

30

30

30

30

30

34

34

34

Zadanie 3.4.

34

34

34

34

34

Zadanie 3.5.

34

34

34

34

Zadanie 3.6.

35

35

35

35

35

35

35

35

35

36

36

Zadanie 2.

36

36

36

36

36

36

46

46

46

Zadanie 4.4.

46

46

46

46

46

46

46

Zadanie 4.6.

46

46

46

46

46

46

Zadanie 4.9.

46

46

46

Zadanie 4.10.

46

46

46

47

47

47

Zadanie 4.14.

47

47

47

47

47

Zadanie 4.17.

47

47

47

47

47

47

Zadanie 4.20.

47

47

47

47

48

48

48

48

48

48

48

48

60

61

61

Zadanie 5.4.

61

61

61

61

Zadanie 5.5.

61

61

61

61

Zadanie 5.6.

61

61

61

61

61

61

Zadanie 5.9.

61

61

61

61

61

61

61

Zadanie 5.13.

61

61

61

62

62

62

62

62

62

62

Zadanie 5.21.

62

62

62

62

62

63

63

63

63

63

Zadanie 5.29.

63

63

63

64

64

64

64

64

73

73

73

73

Zadanie 6.5.

73

73

73

73

Zadanie 6.6.

73

73

73

73

73

73

Zadanie 6.7.

73

73

73

73

74

Zadanie 6.10.

74

74

74

74

74

74

Zadanie 6.14.

74

74

74

Zadanie 6.15.

74

74

74

74

74

74

75

75

75

75

75

75

75

75

75

75

91

92

92

92

92

92

92

92

92

92

92

93

Zadanie 7.13.

93

93

93

93

93

93

93

93

93

93

93

94

94

94

94

94

94

94

94

94

94

95

95

95

95

95

95

95

95

95

95

96

96

96

96

96

96

96

96

96

96

96

101

102

102

102

102

102

102

102

102

102

102

102

103

103

103

103

103

103

103

103

104

104

104

104

104

104

104

105

105

105

105

105

105

105

105

105

105

106

106

106

106

106

106

106

106

106

107

107

107

107

108

108

108

108

108

108

108

Zadanie 38.

108

108

108

108

108

109

109

109

109

109

109

109

109

109

109

110

110

110

110

110

110

Zadanie 56.

110

110

110

110

110

111

111

111

111

111

111

111

111

111

111

112

112

112

112

112

112

112

112

Pełny spis treści