Prosto do matury 4. Zakres podstawowy i rozszerzony. Podręcznik - rozwiązania i odpowiedzi

Podręcznik, Wydawnictwo: Nowa Era

Zadanie 6.17. - strona 74

Wyznacz pole P otrzymanego przekroju, jeśli promień podstawy stożka jest równy $r$ , a tworząca jest nachylona do płaszczyzny podstawy pod kątem $α$ . Przez wierzchołek stożka poprowadzono płaszczyznę, która tworzy z osią symetrii stożka kąt $β$ .

$| AF | = | BF | = r = | FH |, | HI | = | GI | = x, | FI | = y, | C F | = H, | IC | = h$ $tg α = \frac{H}{r}, tg β = \frac{y}{H}$ $H = rtg α, y = Htg β$ $y = rtg α tg β$ $x^{2} + y^{2} = r^{2}$ $x = \sqrt{r^{2} - y^{2}} = \sqrt{r^{2} - r^{2} t g^{2} α t g^{2} β} = r \sqrt{1 - 1 t g^{2} α t g^{2} β}$ $\cos β = \frac{H}{h}$ $h = \frac{H}{\cos β} = \frac{rtg α}{\cos β}$ $P = \frac{1}{2} \cdot \frac{rtg α}{\cos β} \cdot 2 r \sqrt{1 - 1 t g^{2} α t g^{2} β} = \frac{r^{2} tg α \sqrt{1 - 1 t g^{2} α t g^{2} β}}{\cos β}$

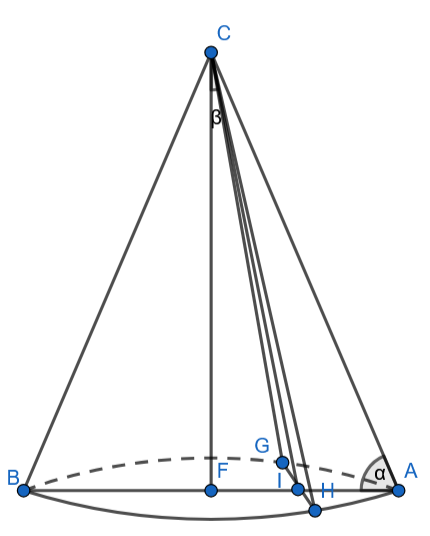
Skorzystaj z funkcji tangens w trójkątach prostokątnych, aby wyznaczyć wysokość stożka i długość odcinka FI. Następnie z twierdzenia Pitagorasa oblicz połowę długości podstawy przekroju, a z funkcji cosinus jego wysokość. Na koniec oblicz pole powstałego przekroju.

Zadanie 27., strona 268, Matematyka. Klasa 7. Podręcznik – rozwiązania i odpowiedzi

Zadanie 11, strona 142, Matematyka z kluczem. Klasa 4. Podręcznik. Część 1 - rozwiązania i odpowiedzi

Zadanie 5.162., strona 135, Matematyka 4. Klasa 4. Zbiór zadań. Zakres rozszerzony - rozwiązania i odpowiedzi

Ćwiczenie 1, strona 18, Matematyka z Plusem. Geometria. Klasa 4. Zeszyt ćwiczeń. Wersja A. Część 2/3 - rozwiązania i odpowiedzi

Zadanie 6, strona 78, Matematyka z plusem. Klasa 7. Podręcznik – rozwiązania i odpowiedzi

Zadanie 2., strona 298, Matematyka wokół nas. Klasa 8. Podręcznik - rozwiązania i odpowiedzi

Zadanie 29, strona 177, Matematyka z plusem. Klasa 2. Podręcznik. Zakres rozszerzony – rozwiązania i odpowiedzi

Ćwiczenie 4, strona 47, Matematyka. Klasa 8. Zeszyt ćwiczeń - rozwiązania i odpowiedzi

Zadanie 40., strona 460, Matematyka. Prosto do matury. Klasa 1. Zakres podstawowy i rozszerzony. Podręcznik - rozwiązania i odpowiedzi

Zadanie 3., strona 29, Prosto do matury. Matematyka. Klasa 2. Podręcznik. Zakres podstawowy i rozszerzony – rozwiązania i odpowiedzi

17

17

17

18

18

18

18

18

18

Zadanie 1.10.

19

19

19

19

Zadanie 1.12.

19

19

19

19

19

19

Zadanie 1.13.

19

19

19

19

19

19

19

19

19

20

20

20

20

Zadanie 2.

20

20

20

20

20

20

20

20

20

27

27

27

Zadanie 2.4.

27

27

27

27

27

27

27

27

Zadanie 2.8.

27

27

27

27

27

28

28

Zadanie 2.11.

28

28

28

28

28

28

Zadanie 2.12.

28

28

28

28

Zadanie 2.14.

28

28

28

28

28

Zadanie 2.15.

29

29

29

29

29

29

Zadanie 2.16.

29

29

29

29

29

Zadanie 2.17.

29

29

29

29

29

Zadanie 2.18.

29

29

29

29

30

30

30

30

30

30

30

30

34

34

34

Zadanie 3.4.

34

34

34

34

34

Zadanie 3.5.

34

34

34

34

Zadanie 3.6.

35

35

35

35

35

35

35

35

35

36

36

Zadanie 2.

36

36

36

36

36

36

46

46

46

Zadanie 4.4.

46

46

46

46

46

46

46

Zadanie 4.6.

46

46

46

46

46

46

Zadanie 4.9.

46

46

46

Zadanie 4.10.

46

46

46

47

47

47

Zadanie 4.14.

47

47

47

47

47

Zadanie 4.17.

47

47

47

47

47

47

Zadanie 4.20.

47

47

47

47

48

48

48

48

48

48

48

48

60

61

61

Zadanie 5.4.

61

61

61

61

Zadanie 5.5.

61

61

61

61

Zadanie 5.6.

61

61

61

61

61

61

Zadanie 5.9.

61

61

61

61

61

61

61

Zadanie 5.13.

61

61

61

62

62

62

62

62

62

62

Zadanie 5.21.

62

62

62

62

62

63

63

63

63

63

Zadanie 5.29.

63

63

63

64

64

64

64

64

73

73

73

73

Zadanie 6.5.

73

73

73

73

Zadanie 6.6.

73

73

73

73

73

73

Zadanie 6.7.

73

73

73

73

74

Zadanie 6.10.

74

74

74

74

74

74

Zadanie 6.14.

74

74

74

Zadanie 6.15.

74

74

74

74

74

74

75

75

75

75

75

75

75

75

75

75

91

92

92

92

92

92

92

92

92

92

92

93

Zadanie 7.13.

93

93

93

93

93

93

93

93

93

93

93

94

94

94

94

94

94

94

94

94

94

95

95

95

95

95

95

95

95

95

95

96

96

96

96

96

96

96

96

96

96

96

101

102

102

102

102

102

102

102

102

102

102

102

103

103

103

103

103

103

103

103

104

104

104

104

104

104

104

105

105

105

105

105

105

105

105

105

105

106

106

106

106

106

106

106

106

106

107

107

107

107

108

108

108

108

108

108

108

Zadanie 38.

108

108

108

108

108

109

109

109

109

109

109

109

109

109

109

110

110

110

110

110

110

Zadanie 56.

110

110

110

110

110

111

111

111

111

111

111

111

111

111

111

112

112

112

112

112

112

112

112

Pełny spis treści