Zadanie
Udowodnij, że przekrój czworościanu jest równoległobokiem, jeśli przez punkty D i E leżące na krawędziach odpowiednio AW i BW czworościanu ABCW poprowadzono płaszczyznę równoległą do krawędzi CW. Wiadomo, że i .
Rozwiązanie
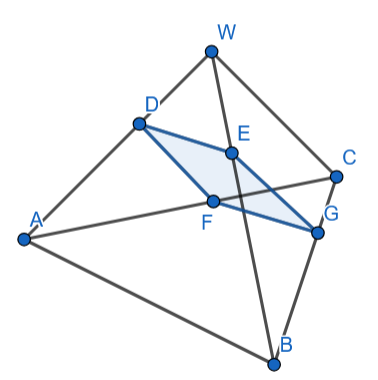– krawędź czworościanu
Trójkąty ABW i DWE są podobne z cechy KKK. Więc:
Płaszczyzna DEFG jest równoległa do krawędzi CW, więc trójkąty DEW i FGC są przystające:
Trójkąty EBG i CBW oraz DAF i WAC są podobne z cechy KKK. Więc:
Czworokąt o bokach: – ma dwie pary takich samych równoległych boków, więc jest równoległobokiem.
To kończy dowód.
Matematyka - wybrane pytania
REKLAMA
Zadania z tego działu
1. Stereometria
7
1. Proste i płaszczyzny w przestrzeni
8
Zadanie 1.10.
19Zadanie 1.12.
19Zadanie 1.13.
19Zadanie 2.
20
2. Kąt nachylenia prostej do płaszczyzny
21
Zadanie 2.4.
27Zadanie 2.8.
27Zadanie 2.11.
28Zadanie 2.12.
28Zadanie 2.14.
28Zadanie 2.15.
29Zadanie 2.16.
29Zadanie 2.17.
29Zadanie 2.18.
29
3. Kąt dwuścienny
31
Zadanie 3.4.
34Zadanie 3.5.
34Zadanie 3.6.
35Zadanie 2.
36
4. Graniastosłupy
37
Zadanie 4.4.
46Zadanie 4.6.
46Zadanie 4.9.
46Zadanie 4.10.
46Zadanie 4.14.
47Zadanie 4.17.
47Zadanie 4.20.
47
5. Ostrosłupy
49
Zadanie 5.4.
61Zadanie 5.5.
61Zadanie 5.6.
61Zadanie 5.9.
61Zadanie 5.13.
61Zadanie 5.21.
62Zadanie 5.29.
63
6. Bryły obrotowe
65
Zadanie 6.5.
73Zadanie 6.6.
73Zadanie 6.7.
73Zadanie 6.10.
74Zadanie 6.14.
74Zadanie 6.15.
74
7. Pola powierzchni i objętości brył
78
Zadanie 7.13.
93
8. Zadania optymalizacyjne
97
9. Powtórzenie
104
Zadanie 38.
108Zadanie 56.
110