Prosto do matury 4. Zakres podstawowy i rozszerzony. Podręcznik - rozwiązania i odpowiedzi

Podręcznik, Wydawnictwo: Nowa Era

Zadanie 7.25. - strona 94

Oblicz objętość i pole powierzchni bocznej tego ostrosłupa, jeśli w ostrosłupie prawidłowym trójkątnym krawędź podstawy ma długość $a$ . Płaszczyzna przechodząca przez krawędź podstawy i środek wysokości tego ostrosłupa jest nachylona do płaszczyzny podstawy pod kątem $α$ .

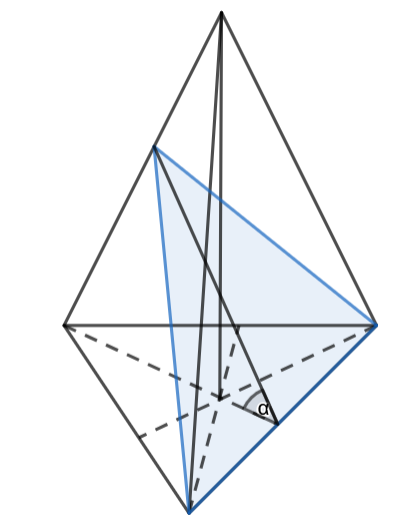$H$ – wysokość ostrosłupa $h$ - wysokość ściany bocznej $h_{p}$ – wysokość podstawy $h_{p} = \frac{a \sqrt{3}}{2}$ $tg α = \frac{\frac{H}{2}}{\frac{1}{3} h_{p}}$ $H = \frac{2}{3} \cdot \frac{a \sqrt{3}}{2} \cdot tg α = \frac{a \sqrt{3}}{3} tg α$ ${(\frac{a \sqrt{3}}{3} tg α)}^{2} + {(\frac{1}{3} \cdot \frac{a \sqrt{3}}{2})}^{2} = h^{2}$ $h = \sqrt{\frac{a^{2}}{3} t g^{2} α + \frac{a^{2}}{12}} = \sqrt{\frac{{12 a}^{2}}{36} t g^{2} α + \frac{3 a^{2}}{36}} = \frac{\sqrt{3} a \sqrt{4 t g^{2} α + 1}}{6}$ $V = \frac{1}{3} \cdot \frac{a^{2} \sqrt{3}}{4} \cdot \frac{a \sqrt{3}}{3} tg α = \frac{a^{3} tg α}{12}$ $P_{B} = 3 \cdot \frac{1}{2} \cdot a \cdot \frac{\sqrt{3} a \sqrt{4 t g^{2} α + 1}}{6} = \frac{\sqrt{3} a^{2} \sqrt{4 t g^{2} α + 1}}{4}$

Zauważ, że $\frac{1}{3}$ wysokości podstawy, wysokość ostrosłupa i wysokość ściany bocznej tworzą trójkąt prostokątny – skorzystaj z funkcji tangens, aby obliczyć wysokość ostrosłupa, a następnie z twierdzenia Pitagorasa, aby wyznaczyć wysokość ściany bocznej. Na koniec oblicz objętość i pole boczne bryły.

Ćwiczenie 3., strona 413, Matematyka. Klasa 1. Podręcznik. Zakres podstawowy - rozwiązania i odpowiedzi

Zadanie 1.164., strona 35, Matematyka. Klasa 3. Zbiór zadań. Zakres rozszerzony – rozwiązania i odpowiedzi

Zadanie 7, strona 106, Matematyka wokół nas. Klasa 6. Podręcznik – rozwiązania i odpowiedzi

Zadanie 18, strona 115, Matematyka z plusem. Klasa 8. Podręcznik – rozwiązania i odpowiedzi

Zadanie Co było na lekcji 12, strona 85, Matematyka. Klasa 6. Zeszyt ćwiczeń. Część 1 - rozwiązania i odpowiedzi

Zadanie 3.14., strona 454, Matematyka. Prosto do matury. Klasa 1. Zakres podstawowy i rozszerzony. Podręcznik - rozwiązania i odpowiedzi

Zadanie branżowe 2., strona 104, To się liczy! Klasa 1. Podręcznik – rozwiązania i odpowiedzi

Zadanie 16, strona 131, NOWA MATeMAtyka. Klasa 1. Zakres podstawowy - rozwiązania i odpowiedzi

Ćwiczenie 3., strona 47, Matematyka z plusem. Liczby naturalne. Klasa 4. Zeszyt ćwiczeń. Wersja A. Część 1/3 - rozwiązania i odpowiedzi

Ćwiczenie 5., strona 26, Matematyka. Klasa 7. Podręcznik – rozwiązania i odpowiedzi

17

17

17

18

18

18

18

18

18

Zadanie 1.10.

19

19

19

19

Zadanie 1.12.

19

19

19

19

19

19

Zadanie 1.13.

19

19

19

19

19

19

19

19

19

20

20

20

20

Zadanie 2.

20

20

20

20

20

20

20

20

20

27

27

27

Zadanie 2.4.

27

27

27

27

27

27

27

27

Zadanie 2.8.

27

27

27

27

27

28

28

Zadanie 2.11.

28

28

28

28

28

28

Zadanie 2.12.

28

28

28

28

Zadanie 2.14.

28

28

28

28

28

Zadanie 2.15.

29

29

29

29

29

29

Zadanie 2.16.

29

29

29

29

29

Zadanie 2.17.

29

29

29

29

29

Zadanie 2.18.

29

29

29

29

30

30

30

30

30

30

30

30

34

34

34

Zadanie 3.4.

34

34

34

34

34

Zadanie 3.5.

34

34

34

34

Zadanie 3.6.

35

35

35

35

35

35

35

35

35

36

36

Zadanie 2.

36

36

36

36

36

36

46

46

46

Zadanie 4.4.

46

46

46

46

46

46

46

Zadanie 4.6.

46

46

46

46

46

46

Zadanie 4.9.

46

46

46

Zadanie 4.10.

46

46

46

47

47

47

Zadanie 4.14.

47

47

47

47

47

Zadanie 4.17.

47

47

47

47

47

47

Zadanie 4.20.

47

47

47

47

48

48

48

48

48

48

48

48

60

61

61

Zadanie 5.4.

61

61

61

61

Zadanie 5.5.

61

61

61

61

Zadanie 5.6.

61

61

61

61

61

61

Zadanie 5.9.

61

61

61

61

61

61

61

Zadanie 5.13.

61

61

61

62

62

62

62

62

62

62

Zadanie 5.21.

62

62

62

62

62

63

63

63

63

63

Zadanie 5.29.

63

63

63

64

64

64

64

64

73

73

73

73

Zadanie 6.5.

73

73

73

73

Zadanie 6.6.

73

73

73

73

73

73

Zadanie 6.7.

73

73

73

73

74

Zadanie 6.10.

74

74

74

74

74

74

Zadanie 6.14.

74

74

74

Zadanie 6.15.

74

74

74

74

74

74

75

75

75

75

75

75

75

75

75

75

91

92

92

92

92

92

92

92

92

92

92

93

Zadanie 7.13.

93

93

93

93

93

93

93

93

93

93

93

94

94

94

94

94

94

94

94

94

94

95

95

95

95

95

95

95

95

95

95

96

96

96

96

96

96

96

96

96

96

96

101

102

102

102

102

102

102

102

102

102

102

102

103

103

103

103

103

103

103

103

104

104

104

104

104

104

104

105

105

105

105

105

105

105

105

105

105

106

106

106

106

106

106

106

106

106

107

107

107

107

108

108

108

108

108

108

108

Zadanie 38.

108

108

108

108

108

109

109

109

109

109

109

109

109

109

109

110

110

110

110

110

110

Zadanie 56.

110

110

110

110

110

111

111

111

111

111

111

111

111

111

111

112

112

112

112

112

112

112

112

Pełny spis treści