Prosto do matury 4. Zakres podstawowy i rozszerzony. Podręcznik - rozwiązania i odpowiedzi

Podręcznik, Wydawnictwo: Nowa Era

Zadanie 74. - strona 112

Oblicz długość krawędzi podstawy takiego ostrosłupa prawidłowego sześciokątnego opisanego na kuli o promieniu 3, którego objętość jest jak najmniejsza.

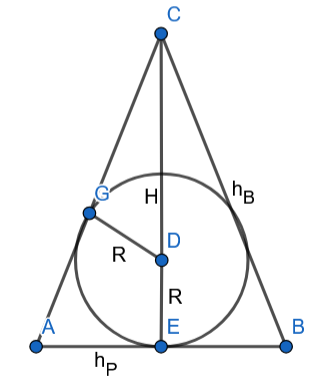
$a$ – krawędź podstawy $H$ – wysokość ostrosłupa $h_{P} = \frac{a \sqrt{3}}{2}$ – wysokość podstawy $h_{B}$ – wysokość ściany bocznej $H^{2} + {(\frac{a \sqrt{3}}{2})}^{2} = h_{B}^{2}$ $h_{B} = \sqrt{H^{2} + \frac{3 a^{2}}{4}}$

Trójkąty AEC i DGC są podobne z cechy KKK.

$\frac{R}{H - R} = \frac{h_{P}}{h_{B}}$ $\frac{3}{H - 3} = \frac{\frac{a \sqrt{3}}{2}}{\sqrt{H^{2} + \frac{3 a^{2}}{4}}}$ $\frac{9}{H^{2} - 6 H + 9} = \frac{\frac{3 a^{2}}{4}}{H^{2} + \frac{3 a^{2}}{4}}$ $9 H^{2} + \frac{27 a^{2}}{4} = \frac{3 a^{2} H^{2}}{4} - \frac{9 a^{2} H}{2} + \frac{27 a^{2}}{4}$ $H^{2} (9 - \frac{3}{4} a^{2}) = \frac{- 9 a^{2} H}{2}$ $H (\frac{36 - 3 a^{2}}{4}) = \frac{- 9 a^{2}}{2}$ $H = \frac{- 36 a^{2}}{72 - 6 a^{2}} = \frac{6 a^{2}}{a^{2} - 12}$ $D : \frac{6 a^{2}}{a^{2} - 12} > 0$ $a > 0$ $V (a) = \frac{1}{3} \cdot 6 \cdot \frac{a^{2} \sqrt{3}}{4} \cdot \frac{6 a^{2}}{a^{2} - 12} = 3 \sqrt{3} \cdot \frac{a^{4}}{a^{2} - 12}$ $V^{'} (a) = \frac{4 a^{3} (a^{2} - 12) - a^{4} \cdot 2 a}{{(a^{2} - 12)}^{2}} = \frac{2 a^{5} - 48 a^{3}}{{(a^{2} - 12)}^{2}}$ $\frac{2 a^{5} - 48 a^{3}}{{(a^{2} - 12)}^{2}} = 0$ $2 a^{3} (a^{2} - 24) = 0$ $2 a^{3} (a - 2 \sqrt{6}) (a + 2 \sqrt{6}) = 0$ $a = 2 \sqrt{6}$

Skorzystaj z twierdzenia Pitagorasa i wyznacz wysokość ściany bocznej. Następnie zauważ, że trójkąty przedstawione na rysunku są podobne. Na tej podstawie zapisz stosunek długości ich krótszych podstaw oraz przeciwprostokątnych i na tej podstawie wyznacz długość wysokości. Wyznacz dziedzinę powstałego wyrażenia, zapisz jako funkcję z niewiadomą $a$ , wyznacz jej pochodną, a następnie miejsce zerowe, aby obliczyć minimalną długość krawędzi podstawy.

Ćwiczenie 7., strona 56, Matematyka z plusem. Klasa 5. Zbiór zadań - rozwiązania i odpowiedzi

Zadanie 8., strona 86, Matematyka z plusem. Klasa 5. Podręcznik - rozwiązania i odpowiedzi

Zadanie branżowe 4., strona 14, To się liczy! Klasa 1. Podręcznik – rozwiązania i odpowiedzi

Zadanie 6, strona 262, MATeMAtyka. Klasa 3. Zbiór zadań. Zakres podstawowy i rozszerzony – rozwiązania i odpowiedzi

Zadanie 4, strona 30, Matematyka z kluczem. Klasa 4. Zbiór zadań – rozwiązania i odpowiedzi

Zadanie 2., strona 324, Prosto do matury. Klasa 3. Zakres podstawowy. Podręcznik - rozwiązania i odpowiedzi

Zadanie 11.13, strona 261, Matematyka i przykłady jej zastosowań. Klasa 1.Podręcznik. Zakres podstawowy i rozszerzony - rozwiązania i odpowiedzi

Zadanie 7, strona 76, Matematyka z kluczem. Klasa 5. Podręcznik. Część 1 - rozwiązania i odpowiedzi

Zadanie 53., strona 362, Prosto do matury. Matematyka. Klasa 1. Zakres podstawowy. Podręcznik - rozwiązania i odpowiedzi

Zadanie 1, strona 76, Matematyka. Klasa 7. Zeszyt ćwiczeń - rozwiązania i odpowiedzi

17

17

17

18

18

18

18

18

18

Zadanie 1.10.

19

19

19

19

Zadanie 1.12.

19

19

19

19

19

19

Zadanie 1.13.

19

19

19

19

19

19

19

19

19

20

20

20

20

Zadanie 2.

20

20

20

20

20

20

20

20

20

27

27

27

Zadanie 2.4.

27

27

27

27

27

27

27

27

Zadanie 2.8.

27

27

27

27

27

28

28

Zadanie 2.11.

28

28

28

28

28

28

Zadanie 2.12.

28

28

28

28

Zadanie 2.14.

28

28

28

28

28

Zadanie 2.15.

29

29

29

29

29

29

Zadanie 2.16.

29

29

29

29

29

Zadanie 2.17.

29

29

29

29

29

Zadanie 2.18.

29

29

29

29

30

30

30

30

30

30

30

30

34

34

34

Zadanie 3.4.

34

34

34

34

34

Zadanie 3.5.

34

34

34

34

Zadanie 3.6.

35

35

35

35

35

35

35

35

35

36

36

Zadanie 2.

36

36

36

36

36

36

46

46

46

Zadanie 4.4.

46

46

46

46

46

46

46

Zadanie 4.6.

46

46

46

46

46

46

Zadanie 4.9.

46

46

46

Zadanie 4.10.

46

46

46

47

47

47

Zadanie 4.14.

47

47

47

47

47

Zadanie 4.17.

47

47

47

47

47

47

Zadanie 4.20.

47

47

47

47

48

48

48

48

48

48

48

48

60

61

61

Zadanie 5.4.

61

61

61

61

Zadanie 5.5.

61

61

61

61

Zadanie 5.6.

61

61

61

61

61

61

Zadanie 5.9.

61

61

61

61

61

61

61

Zadanie 5.13.

61

61

61

62

62

62

62

62

62

62

Zadanie 5.21.

62

62

62

62

62

63

63

63

63

63

Zadanie 5.29.

63

63

63

64

64

64

64

64

73

73

73

73

Zadanie 6.5.

73

73

73

73

Zadanie 6.6.

73

73

73

73

73

73

Zadanie 6.7.

73

73

73

73

74

Zadanie 6.10.

74

74

74

74

74

74

Zadanie 6.14.

74

74

74

Zadanie 6.15.

74

74

74

74

74

74

75

75

75

75

75

75

75

75

75

75

91

92

92

92

92

92

92

92

92

92

92

93

Zadanie 7.13.

93

93

93

93

93

93

93

93

93

93

93

94

94

94

94

94

94

94

94

94

94

95

95

95

95

95

95

95

95

95

95

96

96

96

96

96

96

96

96

96

96

96

101

102

102

102

102

102

102

102

102

102

102

102

103

103

103

103

103

103

103

103

104

104

104

104

104

104

104

105

105

105

105

105

105

105

105

105

105

106

106

106

106

106

106

106

106

106

107

107

107

107

108

108

108

108

108

108

108

Zadanie 38.

108

108

108

108

108

109

109

109

109

109

109

109

109

109

109

110

110

110

110

110

110

Zadanie 56.

110

110

110

110

110

111

111

111

111

111

111

111

111

111

111

112

112

112

112

112

112

112

112

Pełny spis treści