Wiedząc, że czworokąt ABCD jest równoległobokiem, środkiem boku CD jest punkt M, określ jaką częścią powierzchni równoległoboku jest powierzchnia figury ABN.
H – wysokość równoległoboku
h1 – wysokość trójkąta DMN
h2 – wysokość trójkąta ABN
Wiedząc, że ABCD jest równoległobokiem to:
![]()
![]()
Powyższe równości są prawdziwe, ponieważ są to kąty naprzemianległe.
Trójkąty ABN oraz DMN są podobne z cechy KK.
Oblicz skalę podobieństwa k trójkąta ABN oraz DMN:
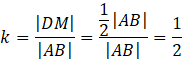
Wyznacz wysokość trójkąta DMN:
![]()
Wyznacz wysokość równoległoboku:
![]()
![]()
![]()
Oblicz pole równoległoboku oraz trójkąta ABN:
![]()
![]()
Oblicz, jaką część pola równoległoboku zajmuje trójkąt ABN:
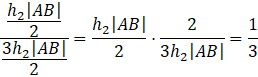

Zauważ, że trójkąty ABN oraz DMN mają dwa takie same kąty, a więc są podobne z cechy KK. Oblicz ich skalę podobieństwa, a następnie uzależnij wysokość trójkąta DMN od wysokości trójkąta ABN. Wyznacz wysokość równoległoboku, korzystając z wysokości trójkątów, a na koniec oblicz pola równoległoboku oraz trójkąta ABN i oblicz, jaką część figury ABCD stanowi trójkąt ABN.

Zadanie 1.
116Zadanie 2.
116Zadanie 3.
117Zadanie 4.
117Zadanie 5.
117Zadanie 9.
118Zadanie 10.
118Zadanie 11.
119Zadanie 12.
119Ćwiczenie B.
121Zadanie 1.
122Zadanie 2.
122Zadanie 3.
122Zadanie 4.
123Zadanie 5.
123Zadanie 6.
123Zadanie 7.
123Zadanie 9.
123Zadanie 11.
124Zadanie 12.
125Zadanie 20.
127Zadanie 21.
127Ćwiczenie A.
128Ćwiczenie B.
129Zadanie 1.
130Zadanie 2.
131Zadanie 3.
131Zadanie 4.
131Zadanie 5.
131Zadanie 6.
132Zadanie 10.
132Zadanie 13.
132Zadanie 14.
133Zadanie 16.
133Zadanie 18.
134Zadanie 1.
135Zadanie 4.
136Zadanie 5.
136Zadanie 9.
137Zadanie 12.
138Ćwiczenie B.
140Zadanie 1.
141Zadanie 3.
141Zadanie 4.
141Zadanie 5.
141Zadanie 6.
142Zadanie 7.
142Zadanie 8.
142
