Wiedząc, że ABC jest trójkątem równobocznym oraz wysokość jest podzielona w stosunku 1 : 3 przez punkt D, określ stosunek |CE| : |EB|.
Załóżmy, wysokość opada na podstawę w punkcie F.
![]()
![]()
Trójkąty FBC oraz CDE są podobne z cechy KK.
Oblicz długość odcinka CD:
![]()
Oblicz skale podobieństwa k:
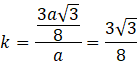
Oblicz długość odcinka CE:
![]()
Oblicz długość odcinka EB:
![]()
Oblicz stosunek |CE| : |EB|:
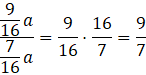
Odpowiedź: Punkt E dzieli bok BC w stosunku 9 : 7

Zauważ, że trójkąty BCF oraz CED mają dwa takie same kąty (kąt prosty oraz |∢DEC|), stąd są podobne z cechy KK. Oblicz długość boku CD oraz skalę podobieństwa (k). Korzystając ze skali podobieństwa oblicz bok CE, a potem EB. Na końcu oblicz stosunek |CE| : |EB|.

Zadanie 1.
116Zadanie 2.
116Zadanie 3.
117Zadanie 4.
117Zadanie 5.
117Zadanie 9.
118Zadanie 10.
118Zadanie 11.
119Zadanie 12.
119Ćwiczenie B.
121Zadanie 1.
122Zadanie 2.
122Zadanie 3.
122Zadanie 4.
123Zadanie 5.
123Zadanie 6.
123Zadanie 7.
123Zadanie 9.
123Zadanie 11.
124Zadanie 12.
125Zadanie 20.
127Zadanie 21.
127Ćwiczenie A.
128Ćwiczenie B.
129Zadanie 1.
130Zadanie 2.
131Zadanie 3.
131Zadanie 4.
131Zadanie 5.
131Zadanie 6.
132Zadanie 10.
132Zadanie 13.
132Zadanie 14.
133Zadanie 16.
133Zadanie 18.
134Zadanie 1.
135Zadanie 4.
136Zadanie 5.
136Zadanie 9.
137Zadanie 12.
138Ćwiczenie B.
140Zadanie 1.
141Zadanie 3.
141Zadanie 4.
141Zadanie 5.
141Zadanie 6.
142Zadanie 7.
142Zadanie 8.
142
