Wiedząc, że przekątne trapezu utworzyły cztery trójkąty, wykaż, że istnieje podobieństwo pomiędzy dwoma z nich.
Nazwij trapez jako ABCD, gdzie AB oraz CD to podstawy. Narysuj przekątne AC oraz BD, a punkt przecięcia nazwij F.
Wiesz, że AB || CD. Kąt AFB jest taki sam jak kąt CFD. Przedłuż przekątną AC oraz podstawy. Kąt BAF jest kątem naprzemianległym kąta DCF, a więc trójkąty ABF oraz CDF są podobne do siebie ze względu na cechę KK.
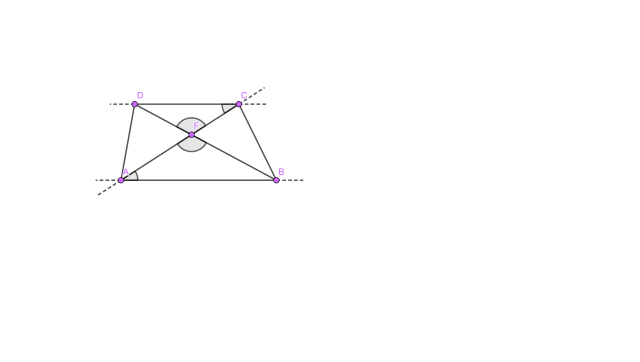

Zauważ, że podstawy i przekątne można potraktować jako dwie proste równoległe przecięte innymi prostymi, więc kąty |∢BAC| oraz |∢DCF| są naprzemianległe, a kąty |∢AFB| oraz |∢DFC| są wierzchołkowe. Wiedząc, to jesteś w stanie udowodnić podobieństwo trójkątów CDF oraz ABF, korzystając z cechy KK.

Zadanie 1.
116Zadanie 2.
116Zadanie 3.
117Zadanie 4.
117Zadanie 5.
117Zadanie 9.
118Zadanie 10.
118Zadanie 11.
119Zadanie 12.
119Ćwiczenie B.
121Zadanie 1.
122Zadanie 2.
122Zadanie 3.
122Zadanie 4.
123Zadanie 5.
123Zadanie 6.
123Zadanie 7.
123Zadanie 9.
123Zadanie 11.
124Zadanie 12.
125Zadanie 20.
127Zadanie 21.
127Ćwiczenie A.
128Ćwiczenie B.
129Zadanie 1.
130Zadanie 2.
131Zadanie 3.
131Zadanie 4.
131Zadanie 5.
131Zadanie 6.
132Zadanie 10.
132Zadanie 13.
132Zadanie 14.
133Zadanie 16.
133Zadanie 18.
134Zadanie 1.
135Zadanie 4.
136Zadanie 5.
136Zadanie 9.
137Zadanie 12.
138Ćwiczenie B.
140Zadanie 1.
141Zadanie 3.
141Zadanie 4.
141Zadanie 5.
141Zadanie 6.
142Zadanie 7.
142Zadanie 8.
142
