Dokonaj konstrukcyjnego podziału odcinka na pięć takich samych fragmentów, wykorzystując wiedzę z ramki.
Konstrukcja:
1. Narysuj dowolny odcinek AB.
2. Narysuj dowolną półprostą wychodzącą z punktu A, tak aby utworzyła kąt mniejszy niż 180° z odcinkiem AB.
3. Wybierz dowolną długość na cyrklu.
4. Odmierz tą długość 5 razy na narysowanej półprostej.
5. Miejsce ostatniego przecięcia łuku z półprostą połącz z punktem B.
6. Przez pozostałe przecięcia łuku z półprostą poprowadź proste równolegle do ostatniego odcinka.
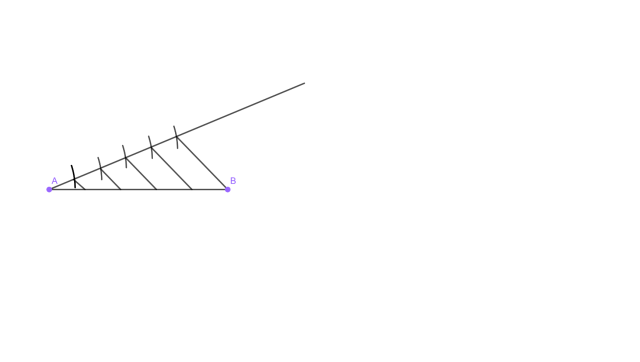

Żeby wykonać tę konstrukcję, musisz wykorzystać twierdzenie Talesa do konstrukcyjnego podziału odcinka na równe części, więcej na ten temat znajduje się w ramce powyżej.

Zadanie 1.
116Zadanie 2.
116Zadanie 3.
117Zadanie 4.
117Zadanie 5.
117Zadanie 9.
118Zadanie 10.
118Zadanie 11.
119Zadanie 12.
119Ćwiczenie B.
121Zadanie 1.
122Zadanie 2.
122Zadanie 3.
122Zadanie 4.
123Zadanie 5.
123Zadanie 6.
123Zadanie 7.
123Zadanie 9.
123Zadanie 11.
124Zadanie 12.
125Zadanie 20.
127Zadanie 21.
127Ćwiczenie A.
128Ćwiczenie B.
129Zadanie 1.
130Zadanie 2.
131Zadanie 3.
131Zadanie 4.
131Zadanie 5.
131Zadanie 6.
132Zadanie 10.
132Zadanie 13.
132Zadanie 14.
133Zadanie 16.
133Zadanie 18.
134Zadanie 1.
135Zadanie 4.
136Zadanie 5.
136Zadanie 9.
137Zadanie 12.
138Ćwiczenie B.
140Zadanie 1.
141Zadanie 3.
141Zadanie 4.
141Zadanie 5.
141Zadanie 6.
142Zadanie 7.
142Zadanie 8.
142
