Dany jest trójkąt prostokątny ABC z okręgiem o środku A, stycznym do boku BC w punkcie P oraz przecinającym odcinek AB w punkcie M, punkt K dzieli bok BC na odcinki |BK| = 2 i |KC| = 4, określ długości BP oraz PC.
Rysunek przedstawia sytuację opisaną w treści zadania:
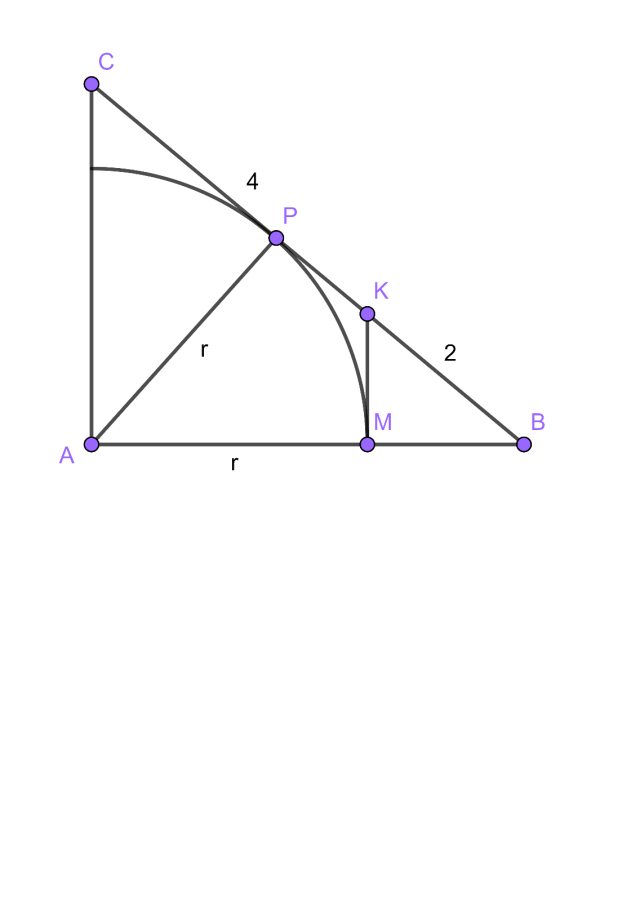
Trójkąty ABC oraz KMB są podobne z cechy KK.
Trójkąty KMB oraz ABP są podobne z cechy KK.
Oblicz skale podobieństwa k pomiędzy ABC, a KMB:
![]()
Oblicz długość boku MB:
![]()
![]()
![]()
Oblicz długość KM korzystając z ich podobieństwa:
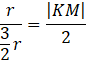
![]()
![]()
Z twierdzenia Pitagorasa oblicz długość r:
![]()
![]()
![]()
![]()
![]()
Oblicz długość AB:
![]()
Oblicz długość PB korzystając z twierdzenia Pitagorasa:
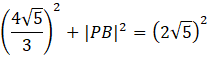
![]()
![]()
![]()
Oblicz długość PC:
![]()

Zauważ, że trójkąty ABC, KMB oraz ABP mają dwa takie same kąty, a więc są podobne z cechy KK. Oblicz skalę podobieństwa ABC oraz KMB, a następnie wyznacz długość boku MB. Długość boku KM możesz obliczyć, tworząc odpowiednią proporcję. Wykorzystaj twierdzenie Pitagorasa na trójkącie KMB, aby obliczyć r. Oblicz długość odcinka AB, a następnie wykorzystaj twierdzenie Pitagorasa na trójkącie APB, aby obliczyć długość PB. Używając odcinka PB, oblicz odcinek PC.

Zadanie 1.
116Zadanie 2.
116Zadanie 3.
117Zadanie 4.
117Zadanie 5.
117Zadanie 9.
118Zadanie 10.
118Zadanie 11.
119Zadanie 12.
119Ćwiczenie B.
121Zadanie 1.
122Zadanie 2.
122Zadanie 3.
122Zadanie 4.
123Zadanie 5.
123Zadanie 6.
123Zadanie 7.
123Zadanie 9.
123Zadanie 11.
124Zadanie 12.
125Zadanie 20.
127Zadanie 21.
127Ćwiczenie A.
128Ćwiczenie B.
129Zadanie 1.
130Zadanie 2.
131Zadanie 3.
131Zadanie 4.
131Zadanie 5.
131Zadanie 6.
132Zadanie 10.
132Zadanie 13.
132Zadanie 14.
133Zadanie 16.
133Zadanie 18.
134Zadanie 1.
135Zadanie 4.
136Zadanie 5.
136Zadanie 9.
137Zadanie 12.
138Ćwiczenie B.
140Zadanie 1.
141Zadanie 3.
141Zadanie 4.
141Zadanie 5.
141Zadanie 6.
142Zadanie 7.
142Zadanie 8.
142
