W pewnym trójkącie połączono środki dwóch ramion, wykaż równoległość pomiędzy tym odcinkiem, a pozostałym bokiem figury.
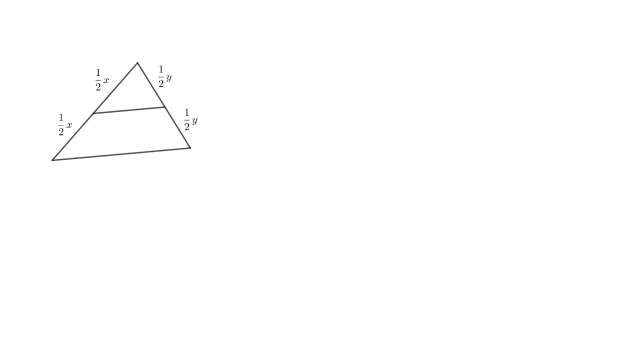
x – długość jednego z boków trójkąta.
y – długość drugiego z boków trójkąta.
Skorzystaj z twierdzenia odwrotnego do twierdzenia Talesa i sprawdź, czy odcinek, dzielący boki na pół, jest równoległy do trzeciego boku:
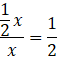

Stąd:
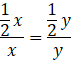
Stąd wynika, że odcinek dzielący boki trójkąta na pół jest równoległy do podstawy. Twierdzenie odwrotne do twierdzenia Talesa jest spełnione.

Zauważ, że możesz wyznaczyć stosunki boków podzielonych przez ten odcinek. Wykorzystaj twierdzenie odwrotne do twierdzenia Talesa, tzn. porównaj obliczone stosunki i jeśli będą takie same, to oznacza, że proste są równoległe.

Zadanie 1.
116Zadanie 2.
116Zadanie 3.
117Zadanie 4.
117Zadanie 5.
117Zadanie 9.
118Zadanie 10.
118Zadanie 11.
119Zadanie 12.
119Ćwiczenie B.
121Zadanie 1.
122Zadanie 2.
122Zadanie 3.
122Zadanie 4.
123Zadanie 5.
123Zadanie 6.
123Zadanie 7.
123Zadanie 9.
123Zadanie 11.
124Zadanie 12.
125Zadanie 20.
127Zadanie 21.
127Ćwiczenie A.
128Ćwiczenie B.
129Zadanie 1.
130Zadanie 2.
131Zadanie 3.
131Zadanie 4.
131Zadanie 5.
131Zadanie 6.
132Zadanie 10.
132Zadanie 13.
132Zadanie 14.
133Zadanie 16.
133Zadanie 18.
134Zadanie 1.
135Zadanie 4.
136Zadanie 5.
136Zadanie 9.
137Zadanie 12.
138Ćwiczenie B.
140Zadanie 1.
141Zadanie 3.
141Zadanie 4.
141Zadanie 5.
141Zadanie 6.
142Zadanie 7.
142Zadanie 8.
142
