Wiedząc, że trójkąt został podzielony, prostą równoległą do jednego z boków, na dwie figury o równych polach, oblicz stosunek długości odcinków podzielonych przez prostą.
Rysunek przedstawia sytuacje z treści zadania:
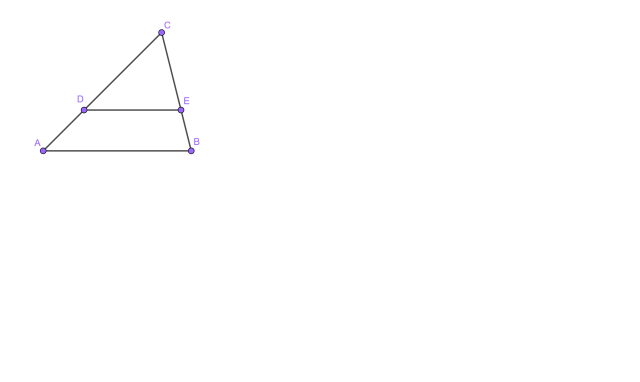
![]()
Trójkąty ABC oraz CDE są podobne z cechy KK.
Oblicz pole trójkąta ABC:
![]()
Oblicz skale podobieństwa k:
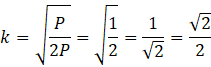
Oblicz długość odcinka CE:
![]()
Oblicz długość odcinka BE:
![]()
Oblicz stosunek boków podzielonych prostą:
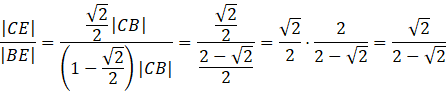
Pozbądź się niewymierności z mianownika mnożąc przez ![]()
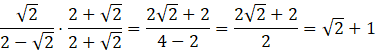
Odpowiedź: Stosunek dwóch odcinków, powstałych przez podzielenie przez prostą, wynosi ![]()

Prosta jest równoległa do podstawy, oznacza to, że kąty |∢CDE| oraz |∢CAB| są takie same. Zauważ, że trójkąty mają dwa takie same kąty, a więc są do siebie podobne z cechy KK. Następnie oblicz skalę podobieństwa (k). Wykorzystując skalę oblicz długość CE oraz BE. Utwórz proporcję z obliczonych boków i rozwiąż ją.

Zadanie 1.
116Zadanie 2.
116Zadanie 3.
117Zadanie 4.
117Zadanie 5.
117Zadanie 9.
118Zadanie 10.
118Zadanie 11.
119Zadanie 12.
119Ćwiczenie B.
121Zadanie 1.
122Zadanie 2.
122Zadanie 3.
122Zadanie 4.
123Zadanie 5.
123Zadanie 6.
123Zadanie 7.
123Zadanie 9.
123Zadanie 11.
124Zadanie 12.
125Zadanie 20.
127Zadanie 21.
127Ćwiczenie A.
128Ćwiczenie B.
129Zadanie 1.
130Zadanie 2.
131Zadanie 3.
131Zadanie 4.
131Zadanie 5.
131Zadanie 6.
132Zadanie 10.
132Zadanie 13.
132Zadanie 14.
133Zadanie 16.
133Zadanie 18.
134Zadanie 1.
135Zadanie 4.
136Zadanie 5.
136Zadanie 9.
137Zadanie 12.
138Ćwiczenie B.
140Zadanie 1.
141Zadanie 3.
141Zadanie 4.
141Zadanie 5.
141Zadanie 6.
142Zadanie 7.
142Zadanie 8.
142
