Skonstruuj taki trójkąt, który został podzielony, na trzy figury o takich samych powierzchniach, przez proste wychodzące z jednego z jego wierzchołków. Wykorzystaj wiedzę z ramki.
Konstrukcja:
1. Narysuj dowolny odcinek i skonstruuj z niego trójkąt równoboczny.
2. Wybierz dowolny odcinek na cyrklu.
3. Wbij nóżkę cyrkla w jeden z wierzchołków podstawy i odznacz ten odcinek 3 razy na ramieniu trójkąta połączonym z danym wierzchołkiem.
4. Ostatnie miejsce przecięcia połącz z drugim wierzchołkiem podstawy.
5. Przez pozostałe miejsca przecięcia poprowadź proste równoległe do utworzonego odcinka.
6. Miejsca przecięcia prostych z podstawą połącz z pozostałym wierzchołkiem.
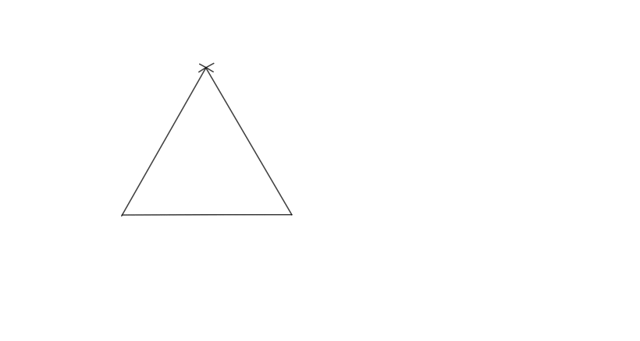
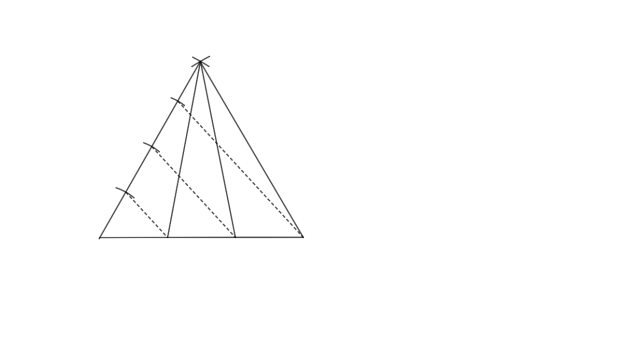

Narysuj dowolny odcinek i skonstruuj trójkąt równoboczny. Wykorzystaj twierdzenie Talesa do konstrukcyjnego podziału podstawy na 3 równe części. Z punktów oznaczających końce odcinków poprowadź proste do jednego z wierzchołków.

Zadanie 1.
116Zadanie 2.
116Zadanie 3.
117Zadanie 4.
117Zadanie 5.
117Zadanie 9.
118Zadanie 10.
118Zadanie 11.
119Zadanie 12.
119Ćwiczenie B.
121Zadanie 1.
122Zadanie 2.
122Zadanie 3.
122Zadanie 4.
123Zadanie 5.
123Zadanie 6.
123Zadanie 7.
123Zadanie 9.
123Zadanie 11.
124Zadanie 12.
125Zadanie 20.
127Zadanie 21.
127Ćwiczenie A.
128Ćwiczenie B.
129Zadanie 1.
130Zadanie 2.
131Zadanie 3.
131Zadanie 4.
131Zadanie 5.
131Zadanie 6.
132Zadanie 10.
132Zadanie 13.
132Zadanie 14.
133Zadanie 16.
133Zadanie 18.
134Zadanie 1.
135Zadanie 4.
136Zadanie 5.
136Zadanie 9.
137Zadanie 12.
138Ćwiczenie B.
140Zadanie 1.
141Zadanie 3.
141Zadanie 4.
141Zadanie 5.
141Zadanie 6.
142Zadanie 7.
142Zadanie 8.
142
