Wiedząc, że bok trójkąta jest podzielony, przez prostą równoległą do AB, na części o wartościach 2 i 5 oraz powierzchnia ABC jest równa 20, określ powierzchnie powstałych figur. Rozważ dwie opcje.
Rysunek przedstawiający pierwszą możliwość:
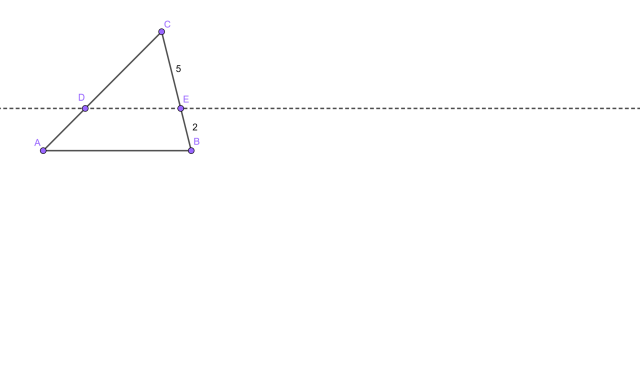
Trójkąty ABC oraz CDE są podobne z cechy KK.
Oblicz skalę podobieństwa k:
![]()
Oblicz pole trójkąta CDE.
![]()
Oblicz pole czworokąta ABED:
![]()
Rysunek przedstawiający drugą możliwość:
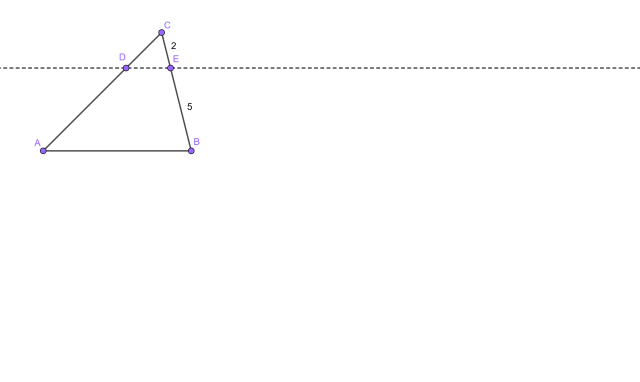
Trójkąty ABC oraz CDE są podobne z cechy KK.
Oblicz skalę podobieństwa k:
![]()
Oblicz pole trójkąta CDE.
![]()
Oblicz pole czworokąta ABED:
![]()

Przez to, że prosta jest równoległa do AB, to kąty |∢CDE| oraz |∢CAB| są takie same. Zauważ, że trójkąty ABC oraz CDE mają dwa takie same kąty, więc są podobne do siebie z cechy KK. Są możliwe dwie opcje, w jednej trójkąt CDE ma bok długości 2, a w drugiej – 5. W obydwu przypadkach oblicz skalę podobieństwa trójkątów CDE i ABC, a następnie wykorzystaj to do obliczenia pola CDE. Możesz to zrobić, mnożąc pole ABC przez podniesioną do kwadratu skalę podobieństwa. Pole ABED obliczysz z różnicy pól ABC oraz CDE.

Zadanie 1.
116Zadanie 2.
116Zadanie 3.
117Zadanie 4.
117Zadanie 5.
117Zadanie 9.
118Zadanie 10.
118Zadanie 11.
119Zadanie 12.
119Ćwiczenie B.
121Zadanie 1.
122Zadanie 2.
122Zadanie 3.
122Zadanie 4.
123Zadanie 5.
123Zadanie 6.
123Zadanie 7.
123Zadanie 9.
123Zadanie 11.
124Zadanie 12.
125Zadanie 20.
127Zadanie 21.
127Ćwiczenie A.
128Ćwiczenie B.
129Zadanie 1.
130Zadanie 2.
131Zadanie 3.
131Zadanie 4.
131Zadanie 5.
131Zadanie 6.
132Zadanie 10.
132Zadanie 13.
132Zadanie 14.
133Zadanie 16.
133Zadanie 18.
134Zadanie 1.
135Zadanie 4.
136Zadanie 5.
136Zadanie 9.
137Zadanie 12.
138Ćwiczenie B.
140Zadanie 1.
141Zadanie 3.
141Zadanie 4.
141Zadanie 5.
141Zadanie 6.
142Zadanie 7.
142Zadanie 8.
142
