W tym zadaniu udowodnij, że jeżeli promień okręgu jest prostopadły do cięciwy, to dzieli ją na pół.
Rysunek pomocniczy:
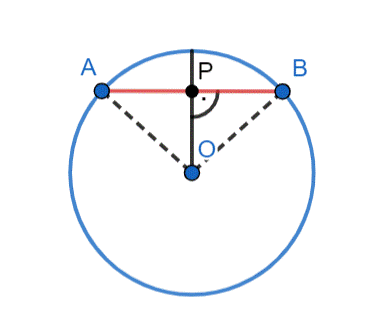
Okrąg O:
promień–r
|AO| = |OB| = r
Zauważ, że trójkąt AOB jest prostokątny, równoramienny
|AO|2 + |OB|2 = |AB|2
r2 + r2 = |AB|2
2r2 = |AB|2 | /√
|AB| = r√2
PAOB = 0,5∙r∙r
PAOB = 0,5r2
PAOB = 0,5∙|OP|∙|AB|
0,5r2 = 0,5∙|OP|∙r√2 / 0,5r
r = |OP|∙√2 | /√2
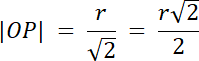
Trójkąt POB–trójkąt prostokątny, więc:
|PB|2 = |OB|2–|OP|2
|PB|2 = r2–0,5r2
|PB|2 = 0,5r2 | /√
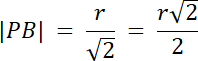
Zauważ, że trójkąty APO i POB są podobne z cech przystawania (bok–bok–bok), więc:
|AP| = |PB|

W tym zadaniu wykorzystaj wzór na pole trójkąta oraz skorzystaj z cech przystawania trójkątów, aby udowodnić tezę.

Ćwiczenie 1.
104Ćwiczenie 2.
105Ćwiczenie 14.
109Zadanie 2.
114Zadanie 3.
114Zadanie 7.
114Ćwiczenie 6.
119Zadanie 2.
120Zadanie 5.
120Ćwiczenie 1.
124Zadanie 1.
126Zadanie 9.
127Zadanie 11.
127Zadanie 1.
135Zadanie 2.
135Zadanie 3.
135Zadanie 4.
135Zadanie 6.
136Zadanie 1.
146Zadanie 3.
146Zadanie 4.
146Zadanie 5.
146Zadanie 7.
146Zadanie 8.
146Ćwiczenie 4.
150Zadanie 3.
151Zadanie 4.
151Zadanie 9.
151Zadanie 10.
151Zadanie 12.
151Ćwiczenie 2.
152Ćwiczenie 4.
155Zadanie 6.
158Zadanie 7.
158Zadanie 9.
159Zadanie 11.
159Zadanie 12.
159Zadanie 17.
159Zadanie 13.
161Zadanie 18.
162Zadanie 20.
162Zadanie 26.
162Zadanie 27.
162
