W tym zadaniu oblicz, w jakiej odległości od symetralnej boku AB znajduje się punkt D.
Rysunek pomocniczy:
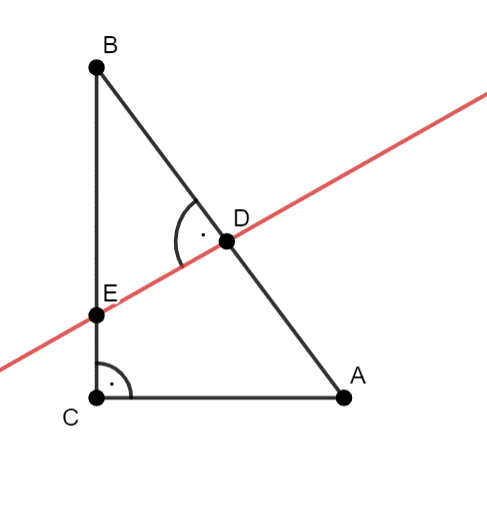
|DE|–symetralna boku AB
|BC|2 = |AB|2–|AC|2
|BC|2 = 102–62
|BC|2 = 100–36
|BC|2 = 64 |/√
|BC| = 8 cm
Zauważ, że:
|BD| = |AD| = 0,5∙|AB|
|BD| = |AD| = 0,5∙10 = 5 cm
Zauważ, że trójkąty ABC i DBE są podobne–cecha podobieństwa (kąt–kąt–kąt), więc:
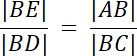
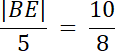
8|BE| = 50 |/8
|BE| = 6,25 cm
|FG| = |BC|–|BE|
|FG| = 8–6,25
|FG| = 1,75 cm

W tym zadaniu wykorzystaj informacje o symetralnej trójkąta oraz cechę podobieństwa trójkątów (kąt–kąt–kąt), a długość boku |BC| wyznacz z twierdzenia Pitagorasa.

Ćwiczenie 1.
104Ćwiczenie 2.
105Ćwiczenie 14.
109Zadanie 2.
114Zadanie 3.
114Zadanie 7.
114Ćwiczenie 6.
119Zadanie 2.
120Zadanie 5.
120Ćwiczenie 1.
124Zadanie 1.
126Zadanie 9.
127Zadanie 11.
127Zadanie 1.
135Zadanie 2.
135Zadanie 3.
135Zadanie 4.
135Zadanie 6.
136Zadanie 1.
146Zadanie 3.
146Zadanie 4.
146Zadanie 5.
146Zadanie 7.
146Zadanie 8.
146Ćwiczenie 4.
150Zadanie 3.
151Zadanie 4.
151Zadanie 9.
151Zadanie 10.
151Zadanie 12.
151Ćwiczenie 2.
152Ćwiczenie 4.
155Zadanie 6.
158Zadanie 7.
158Zadanie 9.
159Zadanie 11.
159Zadanie 12.
159Zadanie 17.
159Zadanie 13.
161Zadanie 18.
162Zadanie 20.
162Zadanie 26.
162Zadanie 27.
162
