W tym zadaniu wyznacz długość odcinka |CP|.
Rysunek pomocniczy:
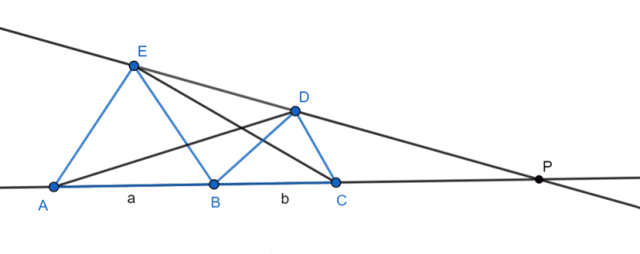
Wyznacz pole trójkąta APE:
PAPE = 0,5∙(|AB| + |BC| + |CP|)∙hABE
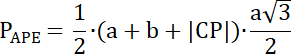
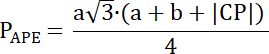
Czworokąt ABDE to trapez, ponieważ |AE| || |BD|–odcinki nachylone są pod kątem 60° do prostej AP.
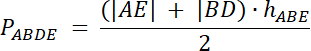
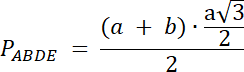
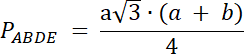
PBPD = 0,5∙|BP|∙hBCD
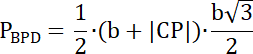
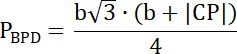
Pole trójkąta APE to suma pól ABDE i BPD, więc:
PAPE = PABCD + PBPD
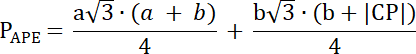
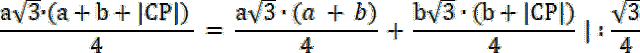
a(a + b + |CP|) = a(a + b) + b(b + |CP)
a2 + ab + a∙|CP| = a2 + ab + b2 + b∙|CP| |–(a2 + ab)
a∙|CP| = b2 + b∙|CP| |–b∙|CP|
a∙|CP|–b∙|CP| = b2
|CP| (a–b) = b2 | /(a–b)
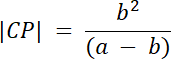

W tym zadaniu wykorzystaj wzór na wysokość w trójkącie równobocznym, a także skorzystaj z własności trapezu–jego podstawy są równoległe wobec siebie. Uwzględnij również informację, pod jakim kątem są nachylone odcinki AE i BD do prostej AP–z informacji, że trójkąty ABE i BCD są równoboczne.

Ćwiczenie 1.
104Ćwiczenie 2.
105Ćwiczenie 14.
109Zadanie 2.
114Zadanie 3.
114Zadanie 7.
114Ćwiczenie 6.
119Zadanie 2.
120Zadanie 5.
120Ćwiczenie 1.
124Zadanie 1.
126Zadanie 9.
127Zadanie 11.
127Zadanie 1.
135Zadanie 2.
135Zadanie 3.
135Zadanie 4.
135Zadanie 6.
136Zadanie 1.
146Zadanie 3.
146Zadanie 4.
146Zadanie 5.
146Zadanie 7.
146Zadanie 8.
146Ćwiczenie 4.
150Zadanie 3.
151Zadanie 4.
151Zadanie 9.
151Zadanie 10.
151Zadanie 12.
151Ćwiczenie 2.
152Ćwiczenie 4.
155Zadanie 6.
158Zadanie 7.
158Zadanie 9.
159Zadanie 11.
159Zadanie 12.
159Zadanie 17.
159Zadanie 13.
161Zadanie 18.
162Zadanie 20.
162Zadanie 26.
162Zadanie 27.
162
