W tym zadaniu oblicz długość okręgu, w którym znajdują się dwa okręgu stycznie zewnętrznie.
Rysunek pomocniczy:
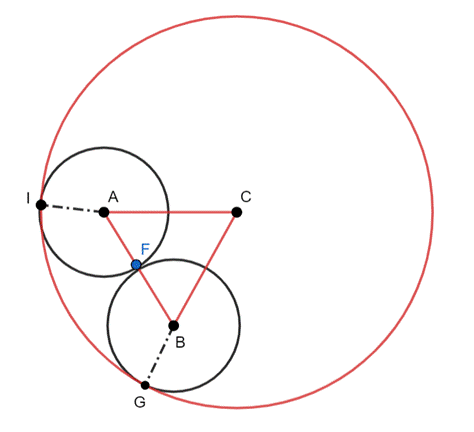
|AF| = |FB| = 4 cm
|AB| = |AF| + |FB|
|AB| = 2|AF|
|AB| = 2∙4 = 8 cm
Trójkąt ABC–trójkąt równoboczny:
|AB| = |BC| = |AC| = 8 cm
Okrąg o środku C:
Promień okręgu: |CG|
|CG| = |CB| + |BG|
|CG| = 8 + 4 = 12 cm
Długość łuku: 2πr = 2π∙12 = 24π cm

W tym zadaniu skorzystaj z własności wzajemnego położenia okręgów, wyznacz promień okręgu o środku C, a następnie jego długość–skorzystaj ze wzoru na długość okręgu.

Ćwiczenie 1.
104Ćwiczenie 2.
105Ćwiczenie 14.
109Zadanie 2.
114Zadanie 3.
114Zadanie 7.
114Ćwiczenie 6.
119Zadanie 2.
120Zadanie 5.
120Ćwiczenie 1.
124Zadanie 1.
126Zadanie 9.
127Zadanie 11.
127Zadanie 1.
135Zadanie 2.
135Zadanie 3.
135Zadanie 4.
135Zadanie 6.
136Zadanie 1.
146Zadanie 3.
146Zadanie 4.
146Zadanie 5.
146Zadanie 7.
146Zadanie 8.
146Ćwiczenie 4.
150Zadanie 3.
151Zadanie 4.
151Zadanie 9.
151Zadanie 10.
151Zadanie 12.
151Ćwiczenie 2.
152Ćwiczenie 4.
155Zadanie 6.
158Zadanie 7.
158Zadanie 9.
159Zadanie 11.
159Zadanie 12.
159Zadanie 17.
159Zadanie 13.
161Zadanie 18.
162Zadanie 20.
162Zadanie 26.
162Zadanie 27.
162
