W tym zadaniu wyznacz wartość liczby c i na tej podstawie określ długości boków w tym trójkącie.
a, b, c–długości boków trójkąta,
a < b + c ∧ b < a + c ∧ c < a + b
Przyjmij:
a = 2–c,
b = 7,
c = 2c + 5
Założenia: 2–c > 0 ∧ 2c + 5 > 0 ∧ c > 0 ∧ c ∊ N⇒ c ∊ (0, 2)
2–c < 7 + 2c + 5 ∧ 7 < 2–c + 2c + 5 ∧ 2c + 5 < 2–c + 2c + 5
2–c < 2c + 12 ∧ 7 < c + 7 ∧ 2c + 5 < c + 7
–10 < 3c ∧ 0 < c ∧ c < 2
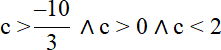
c ∊ (0, 2) ∧ c ∊ N⇒ c = 1
a = 2–1 = 1
b = 7
c = 2∙1 + 5 = 8
Boki tego trójkąta: 1, 7, 8.

W tym zadaniu skorzystaj z twierdzenia o nierówności trójkątów. Zapisz również dziedzinę liczby c.

Ćwiczenie 1.
104Ćwiczenie 2.
105Ćwiczenie 14.
109Zadanie 2.
114Zadanie 3.
114Zadanie 7.
114Ćwiczenie 6.
119Zadanie 2.
120Zadanie 5.
120Ćwiczenie 1.
124Zadanie 1.
126Zadanie 9.
127Zadanie 11.
127Zadanie 1.
135Zadanie 2.
135Zadanie 3.
135Zadanie 4.
135Zadanie 6.
136Zadanie 1.
146Zadanie 3.
146Zadanie 4.
146Zadanie 5.
146Zadanie 7.
146Zadanie 8.
146Ćwiczenie 4.
150Zadanie 3.
151Zadanie 4.
151Zadanie 9.
151Zadanie 10.
151Zadanie 12.
151Ćwiczenie 2.
152Ćwiczenie 4.
155Zadanie 6.
158Zadanie 7.
158Zadanie 9.
159Zadanie 11.
159Zadanie 12.
159Zadanie 17.
159Zadanie 13.
161Zadanie 18.
162Zadanie 20.
162Zadanie 26.
162Zadanie 27.
162
